《2025年初一入学分班必刷卷六年级数学》

3. 用8个球设计一个摸球游戏,使摸到白球和摸不到白球的可能性一样大,摸到红球的可能性比摸到黄球的可能性大,则游戏可设计满足上述条件的白、红、黄球的个数可能分别为(D)
A.4,2,2
B.3,2,3
C.5,2,1
D.4,3,1

答案： D【解析】因为摸到白球与摸不到白球的可能性一样大,所以白球是总数的一半;摸到红球的可能性比摸到黄球的可能性大,所以红球的个数多于黄球的个数,所以D项合适。

1. 如右图,甲转动指针,乙猜指针会停在哪一个数上,如果乙猜对了,乙获胜;如果乙猜错了,甲获胜。

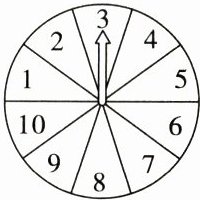
(1)这个游戏规则对双方公平吗?为什么?
(2)乙一定会输吗?
(3)现在有以下四种猜数的方法,如果你是乙,你会选择哪一种?请说明理由。
①不是2的倍数;②不是3的倍数;③大于6的数;④不大于6的数。
(4)你能设计一个公平的游戏规则吗?

答案：
(1)不公平
(2)不一定
(3)第②种
(4)见解析
【解析】
(1)乙获胜的可能性是$1÷10=\frac{1}{10}$,甲获胜的可能性是$\frac{9}{10}$,显然是不公平的。
(2)因为乙获胜的可能性是$\frac{1}{10}$,属于不确定事件中的可能性事件,可能赢,也可能输。
(3)题图中有1,2,3,4,5,6,7,8,9,10共10个数字。①不是2的倍数有1,3,5,7,9共5个,$5÷10=\frac{1}{2}$;②不是3的倍数,有1,2,4,5,7,8,10共7个,$7÷10=\frac{7}{10}$;③大于6的数有7,8,9,10共4个,$4÷10=\frac{2}{5}$;④不大于6的数有1,2,3,4,5,6共6个,$\frac{6}{10}=\frac{3}{5}$。$\frac{7}{10}＞\frac{3}{5}＞\frac{1}{2}＞\frac{2}{5}$,选择②猜中的可能性最高。
(4)设计游戏时只要使双方赢的机会均等就可以。举例:用1~8这8张纸牌,打乱反扣在桌上,每次任意翻出一张,翻到单数算甲赢,翻到双数算乙赢。(合理即可,答案不唯一)

2. 小悦与阿奇比赛下军棋,两人水平相当,两人约定赛7局,先赢4局者胜。现在已经比了3局,小悦胜了2局,阿奇胜了1局。小悦获得最后胜利的概率有多大?

答案： $\frac{11}{16}$【解析】假设不管是否有人先赢4局,都要比满7局,那么之后还要比4局,小悦需要至少胜两局。小悦胜4局有1种,胜3局有4种,胜2局有$4×3÷2=6$(种),共11种可能,概率为$\frac{11}{2^{4}}=\frac{11}{16}$。