《2025年初一入学分班必刷卷六年级数学》

1.(推理)观察下面顺序排列的等式。
9×0+1= 1 9×1+2= 11 9×2+3= 21 9×3+4= 31 …
猜想：第21个等式应为9×20+21=201。

答案： 9×20+21=201

2.(规律)有一列数：1,2,3,5,8,13,21,…从第3个数起,每个数都是前面两个数的和。在前2005个数中,偶数有668个。

答案： 668

3.(规律)有一列数$\frac{1}{2},\frac{3}{5},\frac{5}{10},\frac{7}{17},\frac{9}{26},...$请按照此规律写出第10个数：$\frac{19}{101}$。

答案： $\frac{19}{101}$

4.(排列组合、规律)某赛季欧洲足球冠军联赛淘汰赛共有16支队伍,采取两两配对进行两回合淘汰赛,最后冠军亚军决赛一场决胜负,则一共要进行15场比赛。

答案： 15

5.(推理)规定正整数n的“H运算”是：①当n为奇数时,H= 3n+13；②当n为偶数时,H= $n×\frac{1}{2}×\frac{1}{2}×\frac{1}{2}×...$(其中H为奇数)。如：数3经过1次“H运算”的结果是22；经过2次“H运算”的结果是11；经过3次“H运算”的结果是46。数20经过20次“H运算”的结果是______16。

答案： 16

6.(规律)观察下面的算式,看看你有什么发现。
$1^{3}+2^{3}= 9$ $(1+2)^{2}= 9$
$1^{3}+2^{3}+3^{3}= 36$ $(1+2+3)^{2}= 36$
$1^{3}+2^{3}+3^{3}+4^{3}= 100$ $(1+2+3+4)^{2}= 100$
通过你的发现计算：$1^{3}+2^{3}+3^{3}+4^{3}+... +15^{3}= $14400。

答案： 14400

7.(规律)瑞士中学教师巴尔末成功地从光谱数据$\frac{9}{5},\frac{16}{12},\frac{25}{21},\frac{36}{32},...$中得到巴尔末公式,从而打开了光谱奥妙的大门,请你按这种规律写出第9个数据：$\frac{121}{117}$。

答案： $\frac{121}{117}$

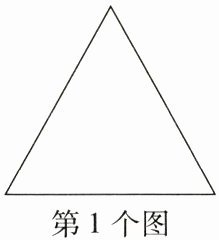
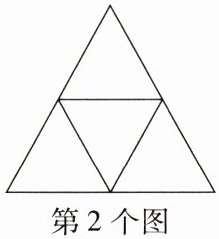
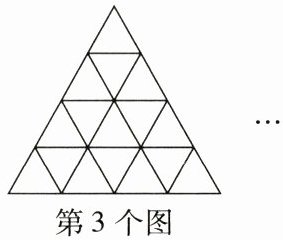
8.(规律)观察下图,按照图中的规律,第5个图中有256个最小的单位三角形。


...

答案： 256