《2025年初一入学分班必刷卷六年级数学》

1. (立方体切拼问题)一个长方体,如果沿水平方向切开,得到两个完全相同的正方体,已知每个正方体的表面积是60平方厘米,则这个长方体的表面积是100平方厘米。

答案： 100 【解析】一个长方体，沿水平方向切开，得到两个完全相同的正方体，说明原来长方体有两个面是正方形，正方体的表面积是60平方厘米，一个面的面积是60÷6 = 10(平方厘米)，原来长方体的表面积 = 10×2×4 + 10×2 = 100(平方厘米)。

2. (正方体的表面积)有一个正方体,如果高增加2厘米,就变成一个长方体,这个长方体的表面积比原来增加了96平方厘米,则原来正方体的表面积为______864平方厘米。

答案： 864 【解析】设原来的正方体的棱长为x厘米，那么高增加2厘米变成长方体后，表面积增加了4个长为x厘米，宽为2厘米的长方形，所以由题可得：4×2×x = 96，解得x = 12，所以这个正方体的表面积为：12×12×6 = 864(平方厘米)。

3. (长方体的表面积)一个长方体的长、宽、高恰好是3个连续的自然数,并且它的体积的数值等于它的所有棱长之和的数值的2倍,那么这个长方体的表面积是______148。

答案： 148 【解析】把中间的棱长设为x，那么剩下的两个长度分别是x + 1，x - 1，列出算式：x×(x + 1)×(x - 1)=(x - 1 + x + x + 1)×4×2，x(x + 1)(x - 1)=24x，(x + 1)·(x - 1)=24，根据24 = 4×6，凑数得到x = 5，棱长分别为4，5，6，表面积是(4×5 + 4×6 + 5×6)×2 = 74×2 = 148。

4. (长方体的体积)长方体的棱长的和是216厘米,它的长、宽、高之比为4:3:2,长方体的体积是5184立方厘米。

答案： 5184 【解析】长方体的棱长的和为216厘米，所以这个长方体一组长、宽、高的和为216÷4 = 54(厘米)，而长、宽、高的比为4:3:2，所以这个长方体的长为54×$\frac{4}{4 + 3 + 2}$= 24(厘米)，宽为54×$\frac{3}{4 + 3 + 2}$= 18(厘米)，高为54×$\frac{2}{4 + 3 + 2}$= 12(厘米)，所以长方体的体积为24×18×12 = 5184(立方厘米)。

5. (长方体的容积)用一张长24厘米、宽23厘米的长方形铁皮,焊接成一个没有盖子的盒子,则焊接的盒子容积最大是______960立方厘米。

答案： 960 【解析】在长方形铁皮四个角减去边长为x cm的正方形，做成长方体盒子，体积为(24 - 2x)(23 - 2x)x。用枚举法来找出其体积最大值。依次代入x的值，可得当x = 4时体积最大，是960立方厘米。所以容积最大是960立方厘米。

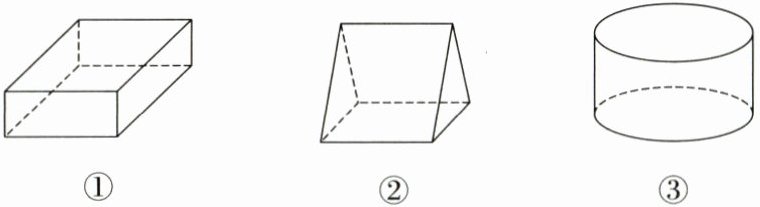
6. (立体图形的分类与识别)如图所示的三个几何体,其中棱柱是①②(填写序号)。

答案： ①② 【解析】有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫做棱柱，观察图中的三个几何体，符合这一特点的是①和②。

7. (组合图形的体积)有一个深12分米的长方体容器,其内侧底面为边长9分米的正方形,当容器底面的一边紧贴桌面倾斜如图时,容器内的水刚好不溢出,那么容器内的水有______升。

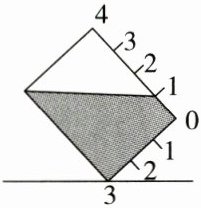
答案：
607.5 【解析】如图所示，在倾斜的容器的四等分线的点1处画平行于底的线，可知上面的三份中，水正好是一半。线下的水正好是容器的$\frac{1}{4}$，而线上部分水正好是容器的$\frac{3}{4}$的$\frac{1}{2}$。所以水占整个容器的$\frac{1}{4}+\frac{3}{4}×\frac{1}{2}=\frac{5}{8}$。所以容器里的水是9×9×12×$\frac{5}{8}$= 607.5(升)。

8. (圆柱的体积、圆锥的体积)一个圆柱的底面周长是一个圆锥的底面周长的$\frac{2}{3}$,而这个圆锥的高是圆柱高的$\frac{2}{5}$,则圆锥的体积是圆柱体积的$\frac{3}{10}$。(填分数)

答案： $\frac{3}{10}$ 【解析】假设圆柱的底面积为S，高为h，则圆锥的底面积为S÷$(\frac{2}{3})^{2}=\frac{9}{4}S$，高为$\frac{2}{5}h$，圆柱的体积为Sh，圆锥的体积为$\frac{1}{3}×\frac{9}{4}S×\frac{2}{5}h=\frac{3}{10}Sh$，$\frac{3}{10}Sh÷Sh=\frac{3}{10}$，所以圆锥的体积是圆柱体积的$\frac{3}{10}$。

9. (圆柱的体积、圆锥的体积)如图是两个底面积相同的圆柱和圆锥形杯子,其中圆柱形杯子的$\frac{2}{5}$盛有水,将水倒入圆锥形的杯子中刚好倒满,则圆柱的高与圆锥的高的比是5:6。

答案： 5:6 【解析】盛有$\frac{2}{5}$水的圆柱形杯子将水倒入圆锥形的杯子中刚好倒满，则圆锥体积是圆柱的体积的$\frac{2}{5}$。所以，设圆柱和圆锥形杯子的底面积为S，圆柱的高为$h_{1}$，圆锥的高为$h_{2}$，则$\frac{1}{3}Sh_{2}=\frac{2}{5}Sh_{1}$，则$h_{1}:h_{2}=5:6$。

10. (圆柱的体积、长方体的体积)用直径为20 cm的圆柱形钢锻造成长、宽、高分别为20 cm、15 cm、5 cm的长方体钢板,应截取圆柱形钢的长为4.8cm。(结果精确到0.1 cm)

答案： 4.8 【解析】这个长方体的体积为20×15×5 = 1500($cm^{3}$)，1500÷[3.14×(20÷2)$^{2}$]≈4.8(cm)。