《2025年初一入学分班必刷卷六年级数学》

26.计算。(6分)
(1)$1 + 520÷ [(1-\frac{12}{17})÷ (1-\frac{5}{6})-1]× (1+\frac{12}{17})$
(2)$1\frac{1}{3}-\frac{7}{12}+\frac{9}{20}-\frac{11}{30}+\frac{13}{42}-\frac{15}{56}+\frac{17}{72}$

答案：

(1) 161

(2) $ 1\frac{1}{9} $

【解析】

(1) 原式 $ = 1 + 520 ÷ (\frac{5}{17} × 6 - 1) × \frac{29}{17} $

$ = 1 + 520 × \frac{17}{13} × \frac{29}{17} $

$ = 1 + 1160 $

$ = 1161 $

(2) 原式 $ = \frac{4}{3} - \frac{7}{12} + \frac{9}{20} - \frac{11}{30} + \frac{13}{42} - \frac{15}{56} + \frac{17}{72} $

$ = 1 + \frac{1}{3} - (\frac{1}{3} + \frac{1}{4}) + (\frac{1}{4} + \frac{1}{5}) - (\frac{1}{5} + \frac{1}{6}) + (\frac{1}{6} + \frac{1}{7}) - (\frac{1}{7} + \frac{1}{8}) + (\frac{1}{8} + \frac{1}{9}) $

$ = 1 + \frac{1}{3} - \frac{1}{3} - \frac{1}{4} + \frac{1}{4} + \frac{1}{5} - \frac{1}{5} - \frac{1}{6} + \frac{1}{6} + \frac{1}{7} - \frac{1}{7} - \frac{1}{8} + \frac{1}{8} + \frac{1}{9} $

$ = 1 + \frac{1}{9} $

$ = 1\frac{1}{9} $

27.(四则运算)某数的$\frac{1}{9}$比1.2的$\frac{1}{4}$多2.1,这个数是多少? (5分)

答案： 21.6

28.(方程的应用)学校组织植树活动,已知在甲处植树的有27人,在乙处植树的有18人。如果要使在甲处植树的人数是在乙处植树人数的2倍,需要从乙处调多少人到甲处? (6分)

答案： 3人

29.(沙漏模型)在正方形ABDC中,E是BD的中点,AE与BC相交于点F,正方形ABDC的面积是12,求三角形CEF的面积。(6分)

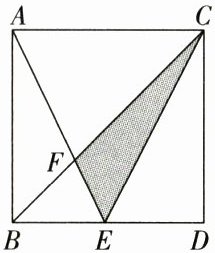
答案： 2