《2025年初一入学分班必刷卷六年级数学》

1. (三角形内角和)如图所示：∠1+∠2+∠3+∠4+∠5+∠6= ______度。

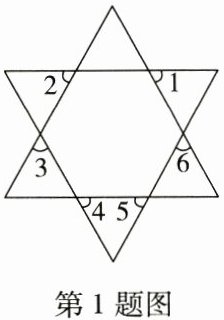
答案：
360 [解析]∠3=∠7,所以∠2+∠3=180°−∠A;同理,∠6=∠8,所以∠1+∠6=180°−∠B;∠4+∠5=180°−∠C;
则∠1+∠2+∠3+∠4+∠5+∠6 =180°×3−(∠A+∠B+∠C)=540°−180°=360°

2. (三角形内角和、比例的应用)一个三角形三个内角的比是3:2:5,这个三角形的三个内角分别是54度、36度、90度,这是一个直角三角形。

答案： 54 36 90 直角 [解析]三角形的内角和为180°，三个内角的度数之比为3:2:5,所以三个内角的度数分别为:180°×$\frac{3}{3+2+5}$=54°;180°×$\frac{2}{3+2+5}$=36°;180°×$\frac{5}{3+2+5}$=90°。因为有一个角为90°的三角形是直角三角形，所以这个三角形是直角三角形。

3. (等腰三角形的性质)如图,点P在直线l上,且AB= BP,除了图上的点P之外,在直线l上最多还可以找到______个点,使它与A,B一起组成等腰三角形的三个顶点。

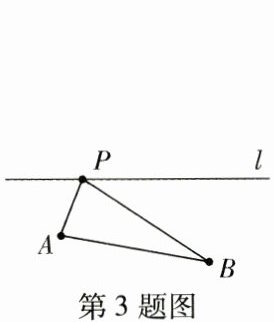
答案：
4 [解析]AB=AP₁,△P₁AB为等腰三角形;AP₂=BP₂,△P₂AB为等腰三角形;AB=AP₃,△P₃AB为等腰三角形;AB=BP₄,△P₄AB为等腰三角形。

4. (线段的性质、比例的应用)如图,点C是线段AB延长线上的一点,且M,N将线段AC分成1:3:4三部分,其中AC= 8/5AB；若MN= 6 cm,则AB= ______10cm。

答案： 10cm [解析]根据题意，设AM为xcm,则MN为3xcm,NC为4xcm,因为MN=6cm,所以3x=6,所以x=2,因为AC=AM+MN+NC=8x,所以AC=8×2=16cm,因为AC=$\frac{8}{5}$AB,所以AB=$\frac{5}{8}$×16=10(cm)。

5. (多边形的对角线)多边形对角线就是多边形任意不相邻两个顶点的连线,如四边形有两条对角线,五边形有五条对角线,那么七边形有______条对角线。

答案：
14 [解析]①在四边形ABCD中与顶点A不相邻的顶点只有(4−3=1,除去它本身和相邻两个点)1个，能画1条对角线;同理每个顶点只能画4−3=1(条)对角线，AC与CA重复，因此四边形有对角线条数为(4−3)×4÷2=2(条)。
②在七边形中，每个顶点可画7−3=4(条)对角线，一共可画(7−3)×7÷2=4×7÷2=14(条)对角线。

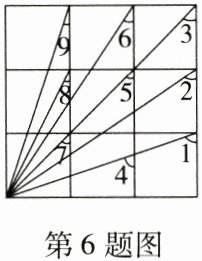
6. (角的计算)如图是一个3×3的正方形,则∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8+∠9= 405°。

答案： 405° [解析]观察图形可知:∠1所在的三角形与∠9所在的三角形全等，∠1与∠9的余角相等，也就是∠1与∠9互余，同理:∠2与∠6互余,∠4与∠8互余,又∠3=∠5=∠7=45°。所以∠1+∠9=90°,∠2+∠6=90°,∠4+∠8=90°,∠3+∠7=90°,∠5=45°。所以∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8+∠9=405°。

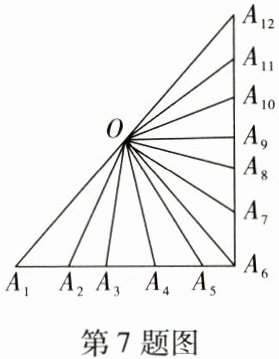
7. (排列组合、三角形的定义)图中一共有37个三角形。

答案： 37 [解析]根据题意，按斜边的中点和它顶角的连线为界，把三角形分成两部分，分别数出两个三角形中的小三角形的个数,A₁A₆边上共有6个点，每两点都可以和O形成一个三角形，一共可以组成5+4+3+2+1=15(个)三角形。A₆A₁₂边上有7个点，每两个点都可以和O形成一个三角形，一共可以组成6+5+4+3+2+1=21(个)三角形,A₁、A₆、A₁₂这三点构成1个最大的三角形，然后相加,即一共有15+21+1=37(个)三角形。

8. (三角形、四边形的概念)若将图1中三角形的个数记为m,图2中的四边形的个数记为n,则m/n= $\frac{4}{5}$。

答案： $\frac{4}{5}$ [解析]图1中三角形的个数为12;图2中四边形的个数为15,所以$\frac{m}{n}$=$\frac{12}{15}$=$\frac{4}{5}$。