《2025年初一入学分班必刷卷六年级数学》

11. (圆锥的体积)如图,将一个圆锥从顶点沿底面直径切成两半后的截面是一个等腰直角三角形,如果圆锥的高是6厘米,则圆锥的体积为______。(π取3.14)

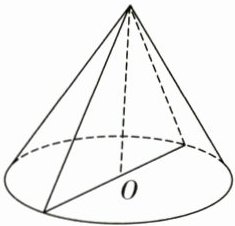
答案：
226.08立方厘米 【解析】圆锥截面是如图的一个等腰直角三角形。在这个三角形中从顶点向下作高是6厘米。三角形的底是圆锥的底面直径，所以圆锥的底面半径和高相等也是6厘米。所以圆锥的体积是3.14×6×6×6÷3 = 226.08(立方厘米)。

12. (代换问题)在一个圆柱体容器里注满水,现在有大、中、小三个铜球。第一次把小球沉入水中;第二次把小球取出,把中球沉入水中;第三次把中球取出,把小球和大球一起沉入水中。已知每次从容器中溢出的水量的情况依次是:第二次是第一次的3倍,第三次是第二次的2.5倍,则大球的体积是小球的______倍。
10.5

答案： 10.5 【解析】第一次溢出的水是小球的体积，设这个溢出水的体积为$V_{1}$，则$V_{小球}=V_{1}$；第二次将小球取出，将中球放进去，那么溢出水的体积是中球的体积减去小球的体积，设这次溢出水的体积为$V_{2}$，则$V_{中球}-V_{小球}=V_{2}$；第三次将中球取出，将大球和小球一起放进去溢出水，设这次溢出水的体积为$V_{3}$，则$V_{大球}+V_{小球}-V_{中球}=V_{3}$。根据题意可知：$V_{2}=3V_{1}$，$V_{3}=2.5V_{2}$，那么可以解得：$V_{小球}=V_{1}$，$V_{中球}=4V_{1}$，$V_{大球}=10.5V_{1}$，所以大球的体积是小球体积的10.5倍。

1. (立体图形的面积与体积)在下面的长方形纸片中,剪出两个圆和一个长方形,恰好可以围成一个圆柱。(π取3.14)
(1)求这个圆柱的体积。
(2)求原长方形纸片的面积。

答案：
(1)785 $cm^{3}$
(2)514 $cm^{2}$ 【解析】
(1)3.14×(10÷2)$^{2}$×10 = 785($cm^{3}$)。答：这个立体图形的体积是785$cm^{3}$。
(2)(3.14×10 + 10×2)×10 = 514($cm^{2}$)。答：原长方形纸片的面积是514$cm^{2}$。

2. (立体图形的面积与体积)把一个长9厘米、宽7厘米、高3厘米的长方体铁块和一个棱长为5厘米的正方体铁块,熔铸成一个底面直径为10厘米的圆柱,为了防锈蚀,要在表面刷上防锈漆,求刷漆的面积。(π取3.14)

答案： 282.6平方厘米 【解析】9×7×3 + 5×5×5 = 314(立方厘米)，10÷2 = 5(厘米)，314÷3.14÷5÷5 = 4(厘米)，3.14×5×5×2 + 3.14×10×4 = 282.6(平方厘米)。答：刷漆的面积是282.6平方厘米。