《2025年课时提优计划作业本九年级物理上册苏科版》

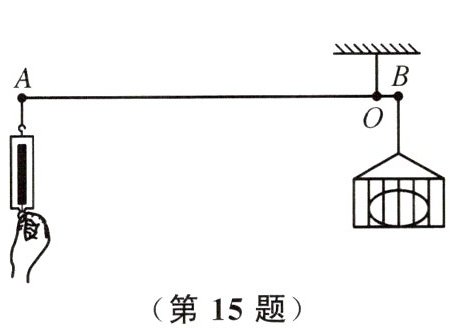
15. 小红和小华用一个弹簧测力计,一根长度为1 m、质量为1.2 kg、粗细均匀、质量分布均匀的圆柱形螺纹钢AB,一个金属筐制成了如图所示的机械装置. 制作时,她们将金属筐系于螺纹钢上的B端,将悬挂螺纹钢的钢索在螺纹钢上的悬吊点移至O点时,螺纹钢在水平位置平衡,测得$ OB = 4 $cm,则金属筐的质量为______kg. 称重时,将重物放入金属筐中,用弹簧测力计竖直向下拉螺纹钢的A端,使之再次在水平位置平衡,此时弹簧测力计的示数为15 N,则重物的质量是______kg. 在她们制作的装置中仅将弹簧测力计换成质量为1 kg的秤砣,制成杆秤,从O点开始,沿OA方向每隔1 cm标出对应的质量刻度,则该杆秤的分度值为______kg. (g取10 N/kg)

答案： 13.8 36 0.25 解析：已知$l_{杆}=1m = 100cm$，$m_{杆}=1.2kg$，螺纹钢AB的重心在AB的中点处，重心到O点的距离$l = 50cm - 4cm = 46cm$，螺纹钢在水平位置平衡，根据杠杆平衡条件可知，$m_{筐}g×OB = m_{杆}g×l$，解得$m_{筐}=13.8kg$；将重物放入金属筐中，用弹簧测力计竖直向下拉螺纹钢的A端，使之再次在水平位置平衡，此时弹簧测力计示数为15N，$OA = 100cm - 4cm = 96cm$，根据杠杆平衡条件可知，$(m_{物}+m_{筐})g×OB = m_{杆}g×l + F×OA$，解得$m_{物}=36kg$；若将弹簧测力计换成质量为1kg的秤砣，根据杠杆的平衡条件可知，当秤砣在A点时，所测物体的重力最大，即质量最大，此时$m_{砣}g×OA = m_{物大}g×OB$，解得$m_{物大}=24kg$，即秤砣在A处时对应的物体的质量为24kg，则该杆秤的分度值为$\frac{24kg}{100 - 4}=0.25kg$.

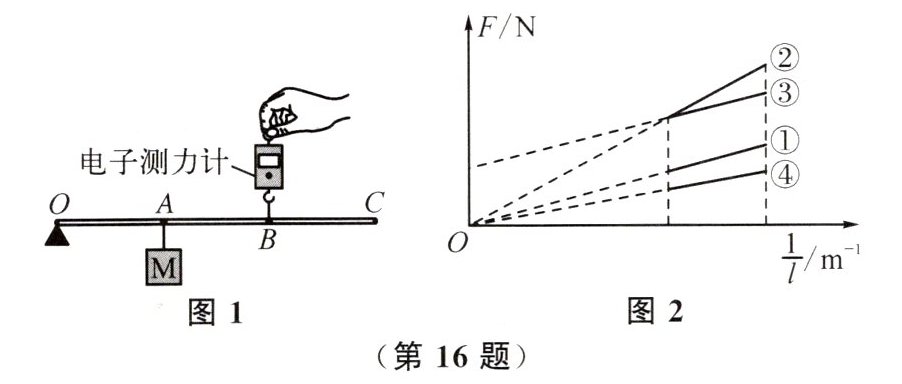
16. 如图1所示,轻质杠杆可绕O点转动,A点悬挂一个重为12 N的物体M,B点受到电子测力计竖直向上的拉力F,杠杆水平静止. 已知$ OA = AB = BC $,则F为______N. 保持杠杆水平静止,将F的作用点从B点移至C点,此过程中F的方向保持不变,F的力臂记为l,则F的大小变______,此时F与$ \frac{1}{l} $的关系图线为图2中的①；若将物体M的悬挂点从A点移至B点后,重复上述操作,则F与$ \frac{1}{l} $的关系图线为图2中的______(选填数字序号).

答案： 6 小 ② 解析：根据杠杆平衡条件有$G×OA = F×OB$，由题意可知，$G = 12N$，$2OA = OB$，代入数据解得$F = 6N$；将F的作用点从B点移至C点，阻力G和阻力臂不变，动力臂逐渐变大，那么动力F将逐渐变小；将M的悬挂点从A点移到B点，则阻力不变，阻力臂变大，那么动力与动力臂的乘积也变大，此时$F×l = G×OB = k$（k值变大），变形得$F=\frac{k}{l}$，说明F和$\frac{1}{l}$成正比例关系，k值变大，则图线斜率变大，图线②符合题意.

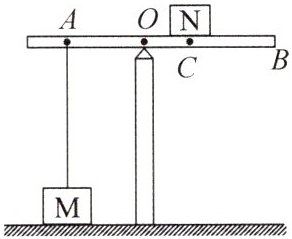
17. 如图所示,一根轻质杠杆水平放在支架上,$ OA = 20 $cm,M重60 N,N重20 N.
(1)已知$ OC = 10 $cm,求绳子的拉力.
(2)当N向右移动,离C点多远可使M对地面的压力恰好为零？

答案： （1）N在C点时，由杠杆平衡条件可得，$F_A×OA = G_N×OC$，即$F_A×20cm = 20N×10cm$，解得$F_A = 10N$，即绳子的拉力为10N （2）当M对地面的压力为零时，绳子的拉力$F_A' = G_M = 60N$，设此时N位于D点，由杠杆平衡条件可得，$F_A'×OA = G_N×OD$，即$60N×20cm = 20N×OD$，解得$OD = 60cm$，即N距离C点的长度$s = OD - OC = 60cm - 10cm = 50cm$

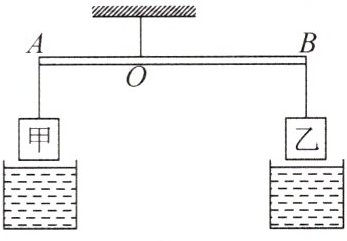
18. 由相同材料制成的甲、乙两个物体分别挂在杠杆A、B两端,O为支点($ OA ＜ OB $),如图所示,杠杆在水平位置平衡. 若将甲、乙两个物体(不溶于水)浸没于水中,则杠杆()

A. A端下沉
B. B端下沉
C. 仍保持平衡
D. 以上说法都不正确

答案： C 解析：由题意可知，甲、乙两个物体的密度相同，根据杠杆的平衡条件可知，$G_{甲}×OA = G_{乙}×OB$，即$ρV_{甲}g×OA = ρV_{乙}g×OB$，所以$V_{甲}×OA = V_{乙}×OB$，如果将甲、乙两个物体（不溶于水）浸没于水中，此时甲、乙都要受到浮力的作用，根据阿基米德原理可知，甲、乙受到的浮力分别为$F_{浮甲}=ρ_水V_{甲}g$、$F_{浮乙}=ρ_水V_{乙}g$，此时杠杆左边拉力与力臂的乘积为$(G_{甲}-ρ_水V_{甲}g)×OA = G_{甲}×OA - ρ_水V_{甲}g×OA$ ①，右边拉力与力臂的乘积为$(G_{乙}-ρ_水V_{乙}g)×OB = G_{乙}×OB - ρ_水V_{乙}g×OB$ ②，由于$V_{甲}×OA = V_{乙}×OB$，所以$ρ_水V_{甲}g×OA = ρ_水V_{乙}g×OB$，则由①②两式可知，此时左、右两边拉力与力臂的乘积仍相等，故杠杆仍然会保持平衡.