《2025年课时提优计划作业本九年级物理上册苏科版》

1. 如图所示,某同学用燃气灶烧水给餐具消毒.已知密闭锅内水的质量为5kg,水的初温为22℃,当水刚好烧开时,共消耗了$0.06m^3$燃气,该燃气灶烧水的热效率为70%.[水的比热容为$4.2×10^3J/(kg·℃),$燃气的热值为$4×10^7J/m^3]$
(1)求$0.06m^3$燃气完全燃烧所放出的热量.
(2)求以上过程中水吸收的热量.
(3)求密闭锅内水烧开时的温度.

答案：
(1) $ Q_{\text{放}} = Vq = 0.06 \, \text{m}^3 \times 4 \times 10^7 \, \text{J/m}^3 = 2.4 \times 10^6 \, \text{J} $
(2) $ Q_{\text{吸}} = \eta Q_{\text{放}} = 70\% \times 2.4 \times 10^6 \, \text{J} = 1.68 \times 10^6 \, \text{J} $
(3) $ \Delta t = \frac{Q_{\text{吸}}}{cm} = \frac{1.68 \times 10^6 \, \text{J}}{4.2 \times 10^3 \, \text{J/(kg·℃)} \times 5 \, \text{kg}} = 80 \, \text{℃} $，$ t = t_0 + \Delta t = 22 \, \text{℃} + 80 \, \text{℃} = 102 \, \text{℃} $
解析：
(1) $ 0.06 \, \text{m}^3 $ 的燃气完全燃烧所放出的热量 $ Q_{\text{放}} = Vq = 0.06 \, \text{m}^3 \times 4 \times 10^7 \, \text{J/m}^3 = 2.4 \times 10^6 \, \text{J} $。
(2) 该燃气灶烧水的热效率 $ \eta = 70\% $，则水吸收的热量 $ Q_{\text{吸}} = \eta Q_{\text{放}} = 70\% \times 2.4 \times 10^6 \, \text{J} = 1.68 \times 10^6 \, \text{J} $。
(3) 水烧开时，水的温度变化量 $ \Delta t = \frac{Q_{\text{吸}}}{cm} = \frac{1.68 \times 10^6 \, \text{J}}{4.2 \times 10^3 \, \text{J/(kg·℃)} \times 5 \, \text{kg}} = 80 \, \text{℃} $，密闭锅内气压高于标准大气压，故水的沸点高于 $ 100 \, \text{℃} $，密闭锅内水烧开时的温度 $ t = t_0 + \Delta t = 22 \, \text{℃} + 80 \, \text{℃} = 102 \, \text{℃} $。

2. 用某煤气灶将质量为5kg的水从20℃加热到100℃,消耗煤气的质量为0.16kg,已知c水$= 4.2×10^3J/(kg·℃),q$煤气$= 4.2×10^7J/kg.$
(1)求水吸收的热量.
(2)求煤气灶烧水的效率.

答案：
(1) 水吸收的热量 $ Q_{\text{吸}} = c_{\text{水}} m_{\text{水}} \Delta t = 4.2 \times 10^3 \, \text{J/(kg·℃)} \times 5 \, \text{kg} \times (100 \, \text{℃} - 20 \, \text{℃}) = 1.68 \times 10^6 \, \text{J} $
(2) 煤气完全燃烧放出的热量 $ Q_{\text{放}} = m q_{\text{煤气}} = 0.16 \, \text{kg} \times 4.2 \times 10^7 \, \text{J/kg} = 6.72 \times 10^6 \, \text{J} $，煤气灶烧水的效率 $ \eta = \frac{Q_{\text{吸}}}{Q_{\text{放}}} \times 100\% = \frac{1.68 \times 10^6 \, \text{J}}{6.72 \times 10^6 \, \text{J}} \times 100\% = 25\% $
解析：见答案。

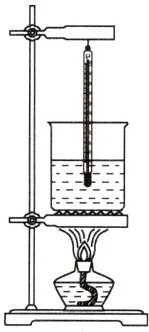
3. (2024·常州)中国工程师利用焦炉气中的氢气与工业尾气中的二氧化碳合成液态燃料,作为第19届亚洲运动会主火炬的燃料.工程师在科普馆用如图所示的装置为同学们演示模拟实验,测量该燃料的热值,操作如下.
①在空酒精灯内加入适量该液态燃料,得到"燃料灯";
②在空烧杯内加入1kg水,测得水的初温为31℃,点燃"燃料灯"开始加热;
③当水恰好沸腾时,立即熄灭"燃料灯",测得"燃料灯"消耗燃料30g.
已知实验时气压为标准大气压,c水$= 4.2×10^3J/(kg·℃),$用该装置加热水的效率为42%.
(1)求此过程中烧杯内的水吸收的热量.
(2)求该液态燃料的热值.

答案：
(1) $ Q_{\text{吸}} = c_{\text{水}} m_{\text{水}} (t - t_0) = 4.2 \times 10^3 \, \text{J/(kg·℃)} \times 1 \, \text{kg} \times (100 \, \text{℃} - 31 \, \text{℃}) = 2.898 \times 10^5 \, \text{J} $
(2) $ Q_{\text{放}} = \frac{Q_{\text{吸}}}{\eta} = \frac{2.898 \times 10^5 \, \text{J}}{42\%} = 6.9 \times 10^5 \, \text{J} $，$ q = \frac{Q_{\text{放}}}{m_{\text{液}}} = \frac{6.9 \times 10^5 \, \text{J}}{30 \times 10^{-3} \, \text{kg}} = 2.3 \times 10^7 \, \text{J/kg} $
解析：
(1) 水吸收的热量 $ Q_{\text{吸}} = c_{\text{水}} m_{\text{水}} (t - t_0) = 4.2 \times 10^3 \, \text{J/(kg·℃)} \times 1 \, \text{kg} \times (100 \, \text{℃} - 31 \, \text{℃}) = 2.898 \times 10^5 \, \text{J} $。
(2) 加热水的效率 $ \eta = 42\% $，则该液态燃料燃烧放出的热量 $ Q_{\text{放}} = \frac{Q_{\text{吸}}}{\eta} = \frac{2.898 \times 10^5 \, \text{J}}{42\%} = 6.9 \times 10^5 \, \text{J} $，热值 $ q = \frac{Q_{\text{放}}}{m_{\text{液}}} = \frac{6.9 \times 10^5 \, \text{J}}{30 \times 10^{-3} \, \text{kg}} = 2.3 \times 10^7 \, \text{J/kg} $。