《2025年课时提优计划作业本九年级物理上册苏科版》

8. 小华用如图所示的装置探究杠杆的机械效率,他将两个钩码悬挂在B点,在A点用弹簧测力计沿竖直方向拉动杠杆,使其绕O点缓慢转动,带动钩码上升一定的高度h(不计摩擦) ()

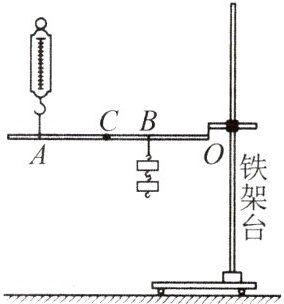
A. 在杠杆转动过程中,弹簧测力计的示数会变小
B. 仅增加钩码的个数,拉力所做的额外功增大
C. 仅将拉力的作用点从A点移到C点,杠杆的机械效率不变
D. 仅将钩码的悬挂点从B点移到C点,拉力做的总功变大

答案： C 解析:弹簧测力计拉力方向始终为竖直向上,阻力不变,动力臂减小,阻力臂变小,根据相似三角形的知识可知,动力臂与阻力臂的比值不变,因为阻力不变,根据杠杆的平衡条件可知,动力不变,即弹簧测力计的示数不变,A错误;克服杠杆重力做的功为额外功,仅增加钩码的个数,杠杆重力和杠杆上升的高度不变,拉力所做的额外功不变,B错误;仅将拉力的作用点从$A$点移到$C$点,钩码和杠杆的重力不变,上升的高度不变,则有用功不变,额外功也不变,总功不变,根据$\eta =\frac{{W}_{有用}}{{W}_{总}}\times 100\%$可知,杠杆的机械效率不变,C正确;仅将钩码的悬挂点从$B$点移到$C$点,钩码还是上升到原来的高度,有用功不变,而杠杆提升的高度变小,克服杠杆重力做的功变小,即额外功变小,所以拉力做的总功变小,D错误.

9. 如图所示,斜面的长为高的4倍,物体恰能在斜面上自由匀速下滑,下滑一段距离的过程中,该物体重力做的功和克服阻力做的功相等. 若用平行于斜面向上的拉力F将物体匀速拉上斜面时,斜面的机械效率为 ()

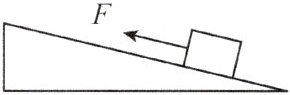
A. 20%
B. 25%
C. 50%
D. 75%

答案： C 解析:物体在斜面上匀速下滑时,重力做的功为${W}_{G}$,克服摩擦力做的功为${W}_{f}$,${W}_{G}={W}_{f}$,当物体被匀速拉上斜面时,物体对斜面的压力和接触面的粗糙程度不变,则物体受到的摩擦力大小不变,此时拉力做的功${W}_{总}={W}_{G}+{W}_{f}=2{W}_{G}$,则机械效率$\eta =\frac{{W}_{G}}{{W}_{总}}\times 100\%=\frac{{W}_{G}}{2{W}_{G}}\times 100\%=50\%$.

10. 如图所示,用手沿竖直方向匀速拉绳,使挂在动滑轮下面重为G的物体缓缓上升,动滑轮的重力不可忽略,现改变物体的重力G,则动滑轮的机械效率$\eta$与物体重力G的关系图像可能为 ()

答案： B 解析:动滑轮的重力不可忽略,则克服绳重、动滑轮的重力和绳与滑轮间的摩擦所做的功为额外功,从摩擦角度考虑,随着物体重力的增大,滑轮与绳子间摩擦增大,则额外功增大;同时,物重增大,有用功也增大,有用功和总功的比值增大,即机械效率逐渐增大,但由于摩擦也在增大,故$\eta$与$G$不成正比,当物重越来越大,有用功远大于额外功时,机械效率无限接近$100\%$,B符合题意.

11. 用如图甲所示的滑轮组做“探究动滑轮的重力对滑轮组机械效率的影响”实验. 实验中把不同的磁铁吸附在动滑轮边框上以改变的滑轮的重力,每次实验都匀速竖直拉动绳端使物体上升10 cm,不计绳重,实验数据如下表所示.

(1) 每次实验中绳端的移动距离为______cm.
(2) 第2次实验中拉力F的示数如图乙所示,为______N;第2次实验中滑轮组的机械效率为______%. 分析数据可知:在物重不变的情况下,动滑轮越重,滑轮组的机械效率越______.
(3) 实验中若仅增大绳端移动的距离,则滑轮组的机械效率将______(选填“变大”“变小”或“不变”).
(4) 本实验中,在物重不变的情况下,动滑轮变重时,由摩擦引起的额外功占总额外功的比例______(选填“变大”“变小”或“不变”).

答案：
(1)$30$
(2)$2.5$ $80$ 低
(3)不变
(4)变小 解析:
(1)由题图甲可知,滑轮组中承重的绳子段数$n=3$,则每次实验中绳端移动的距离$s=3h=3\times 10cm=30cm$.
(2)弹簧测力计的分度值为$0.1N$,示数为$2.5N$;每次实验中的有用功${W}_{有用}={G}_{物}h=6.0N\times 10\times {10}^{-2}m=0.6J$,第2次实验中滑轮组做的总功${W}_{总2}={F}_{2}s=2.5N\times 30\times {10}^{-2}m=0.75J$,则第2次实验中滑轮组的机械效率${\eta }_{2}=\frac{{W}_{有用}}{{W}_{总2}}\times 100\%=\frac{0.6J}{0.75J}\times 100\%=80\%$;分析题表中数据可知,在物重不变的情况下,动滑轮越重,滑轮组的机械效率越低.
(3)实验中若仅增大绳端移动的距离,根据$\eta =\frac{{W}_{有用}}{{W}_{总}}\times 100\%=\frac{{G}_{物}h}{Fs}\times 100\%=\frac{{G}_{物}h}{F\cdot nh}\times 100\%=\frac{{G}_{物}}{nF}\times 100\%$可知,滑轮组的机械效率不变.
(4)实验中由摩擦引起的额外功占总额外功的比例为$\frac{{W}_{摩}}{{W}_{额外}}\times 100\%=\frac{{W}_{总}-{W}_{有用}-{W}_{动}}{{W}_{总}-{W}_{有用}}\times 100\%=\frac{Fs-{G}_{物}h-{G}_{动}h}{Fs-{G}_{物}h}\times 100\%=\frac{3F-{G}_{物}-{G}_{动}}{3F-{G}_{物}}\times 100\%$,代入数据可得,第1、2、3、4次实验中由摩擦引起的额外功占总额外功的比例分别为$50\%$、$33.3\%$、$29.6\%$、$23.8\%$,则在物重不变的情况下,动滑轮变重时,由摩擦引起的额外功占总额外功的比例变小.