第76页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
15. A、B两个物体质量相等,温度均为$10^{\circ }C$;甲、乙两杯中水的质量相等,温度均为$50^{\circ }C$.现将A放入甲杯,B放入乙杯,热平衡后甲杯水温降低了$4^{\circ }C$,乙杯水温降低了$8^{\circ }C$,不考虑热量的损耗,则A、B两个物体的比热容之比为 ()
A. $4:9$
B. $3:5$
C. $2:3$
D. $1:2$
A. $4:9$
B. $3:5$
C. $2:3$
D. $1:2$
答案:
A 解析:热平衡后,物体A与甲杯中水的温度相同,均为$50^{\circ }C-4^{\circ }C=46^{\circ }C$,物体B与乙杯中水的温度相同,均为$50^{\circ }C-8^{\circ }C=42^{\circ }C$,由题意可知,$Q_{A吸}=Q_{甲水放},Q_{B吸}=Q_{乙水放}$,即$mc_{A}×(46^{\circ }C-10^{\circ }C)=m_{水}c_{水}×4^{\circ }C$ ①,$mc_{B}×(42^{\circ }C-10^{\circ }C)=m_{水}c_{水}×8^{\circ }C$ ②,联立①②,解得$c_{A}:c_{B}=4:9$.
16. (2023·常州)家用小型风力发电机独特的尾翼结构能使其旋翼自动迎风,如图甲所示.在海边,仅在海陆风的影响下,图乙、图丙所示的情景通常分别发生在 ()

A. 白天、夜晚
B. 夜晚、白天
C. 白天、白天
D. 夜晚、夜晚

A. 白天、夜晚
B. 夜晚、白天
C. 白天、白天
D. 夜晚、夜晚
答案:
A 解析:题图乙中,发电机的旋翼朝向大海,说明此时风从大海吹向陆地,由于海水的比热容较大,白天时陆地比大海升温快,地面的热空气上升,风从大海吹向陆地,故题图乙所示的情景通常发生在白天;题图丙中,发电机的旋翼朝向陆地,说明此时风从陆地吹向大海,由于海水的比热容较大,夜晚时陆地比大海降温快,海面的热空气上升,风从陆地吹向大海,故题图丙所示的情景通常发生在夜晚.A符合题意.
17. (2024·成都)某固态物质的质量为$m$,比热容为$c$,用稳定的热源对它加热(物质在相同时间内吸收的热量相等),到$t_{3}$时刻停止加热,然后让其冷却.在上述过程中记录不同时刻的温度,最后绘制出温度随时间变化的关系图像(如图所示).下列说法正确的是 ()

A. 在$0\sim t_{2}$时间段,该物质吸收的热量为$cm(T_{2}-T_{1})$
B. 在$t_{2}\sim t_{4}$时间段,该物质的比热容先增大后减小
C. 在$t_{4}\sim t_{5}$时间段,该物质放出的热量为$\frac {cm(T_{2}-T_{1})(t_{5}-t_{4})}{t_{1}}$
D. 该物质在$t_{5}\sim t_{6}时间段的比热容等于在0\sim t_{1}$时间段的比热容

A. 在$0\sim t_{2}$时间段,该物质吸收的热量为$cm(T_{2}-T_{1})$
B. 在$t_{2}\sim t_{4}$时间段,该物质的比热容先增大后减小
C. 在$t_{4}\sim t_{5}$时间段,该物质放出的热量为$\frac {cm(T_{2}-T_{1})(t_{5}-t_{4})}{t_{1}}$
D. 该物质在$t_{5}\sim t_{6}时间段的比热容等于在0\sim t_{1}$时间段的比热容
答案:
D 解析:在$0\sim t_{1}$时间段,物质的温度从$T_{1}$升高到$T_{2}$,则该物质吸收的热量$Q_{吸1}=cm(T_{2}-T_{1})$,在$t_{1}\sim t_{2}$时间段,物质处于熔化阶段,温度不变但持续吸热,故在$0\sim t_{2}$时间段,该物质吸收的热量大于$cm(T_{2}-T_{1})$,A错误;$t_{2}\sim t_{4}$时间段内,物质处于液态,比热容不变,B错误;在$0\sim t_{1}$时间段,单位时间内物质吸收的热量为$\frac {cm(T_{2}-T_{1})}{t_{1}}$,该物质的熔化过程持续时间为$t_{2}-t_{1}$,则该物质在熔化过程中吸收的热量$Q_{熔化吸}=\frac {cm(T_{2}-T_{1})}{t_{1}}×(t_{2}-t_{1})$,该物质在$t_{4}\sim t_{5}$时间段处于凝固过程,对一定质量的晶体来说,凝固时放出的热量与熔化时吸收的热量相等,所以在$t_{4}\sim t_{5}$时间段,该物质放出的热量$Q_{凝固放}=Q_{熔化吸}=\frac {cm(T_{2}-T_{1})}{t_{1}}×(t_{2}-t_{1})$,C错误;该物质在$t_{5}\sim t_{6}$和$0\sim t_{1}$时间段内均处于固态,因此比热容相等,D正确.
18. 阅读短文,回答问题.
牛顿冷却定律
当一个物体表面的温度比周围环境温度高时,就会向周围环境散热,散热快慢可以用单位时间内散失热量的多少来表示.英国物理学家牛顿提出:物体散热快慢与物体和周围环境的温度差成正比.后人研究发现,在温度差不太大的情况下(小于$15^{\circ }C$),这个结论符合实际散热规律,它被称为牛顿冷却定律.若散热快慢用$q$表示,则牛顿冷却定律可以表示为$q= k(t_{物}-t_{环})$,其中$k$是散热系数,与物体的表面性质、表面积、周围环境的性质等因素有关,和物质种类无关,如果上述因素相同,不同物质的散热系数就相同.由于不同物质的比热容不同,则即使散热快慢相同,它们降低相同温度需要的时间也不同,根据降温时间可以得到两种物质比热容的大小关系,从而可以进行比热容的测量.
(1)物体向周围环境散热,内能减小,这种改变内能的方式叫作______.
(2)下列物理量中物理意义和散热快慢$q$类似的有 ()
A. 速度
B. 密度
C. 功率
D. 效率
(3)一个物体的温度为$30^{\circ }C$,周围环境温度保持$20^{\circ }C$不变,此时物体的散热快慢为$q$.当物体温度降低到$29^{\circ }C$时,散热快慢为______.
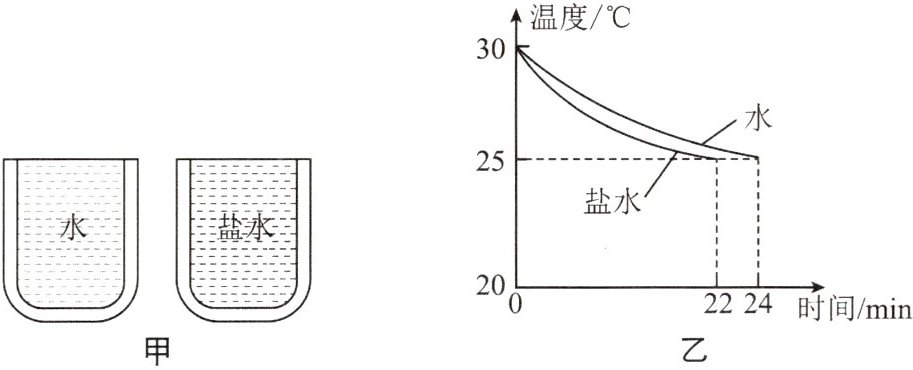
(4)如图甲所示,两个相同的保温杯分别装满水和盐水,水和盐水的温度都是$30^{\circ }C$,周围环境温度保持$20^{\circ }C$不变,保温杯敞开口,水和盐水的温度随时间变化的关系图像如图乙所示.已知水的比热容为$4.2×10^{3}J/(kg\cdot ^{\circ }C)$,水的密度为$1×10^{3}kg/m^{3}$,盐水的密度为$1.1×10^{3}kg/m^{3}$,则盐水的比热容为______$J/(kg\cdot ^{\circ }C)$.
牛顿冷却定律
当一个物体表面的温度比周围环境温度高时,就会向周围环境散热,散热快慢可以用单位时间内散失热量的多少来表示.英国物理学家牛顿提出:物体散热快慢与物体和周围环境的温度差成正比.后人研究发现,在温度差不太大的情况下(小于$15^{\circ }C$),这个结论符合实际散热规律,它被称为牛顿冷却定律.若散热快慢用$q$表示,则牛顿冷却定律可以表示为$q= k(t_{物}-t_{环})$,其中$k$是散热系数,与物体的表面性质、表面积、周围环境的性质等因素有关,和物质种类无关,如果上述因素相同,不同物质的散热系数就相同.由于不同物质的比热容不同,则即使散热快慢相同,它们降低相同温度需要的时间也不同,根据降温时间可以得到两种物质比热容的大小关系,从而可以进行比热容的测量.
(1)物体向周围环境散热,内能减小,这种改变内能的方式叫作______.
(2)下列物理量中物理意义和散热快慢$q$类似的有 ()
A. 速度
B. 密度
C. 功率
D. 效率
(3)一个物体的温度为$30^{\circ }C$,周围环境温度保持$20^{\circ }C$不变,此时物体的散热快慢为$q$.当物体温度降低到$29^{\circ }C$时,散热快慢为______.
(4)如图甲所示,两个相同的保温杯分别装满水和盐水,水和盐水的温度都是$30^{\circ }C$,周围环境温度保持$20^{\circ }C$不变,保温杯敞开口,水和盐水的温度随时间变化的关系图像如图乙所示.已知水的比热容为$4.2×10^{3}J/(kg\cdot ^{\circ }C)$,水的密度为$1×10^{3}kg/m^{3}$,盐水的密度为$1.1×10^{3}kg/m^{3}$,则盐水的比热容为______$J/(kg\cdot ^{\circ }C)$.

答案:
(1)热传递
(2)AC
(3)$\frac {9}{10}q$
(4)$3.5×10^{3}$ 解析:
(1)物体向周围环境散热,物体的内能转移到周围环境温度较低的物体上,内能减小,这种改变内能的方式是热传递.
(2)q是表示散热快慢的物理量,速度是表示物体运动快慢的物理量,功率是表示做功快慢的物理量,这三者的物理意义类似.
(3)当物体的温度为$30^{\circ }C$,周围环境温度为$20^{\circ }C$时,根据牛顿冷却定律$q=k(t_{物}-t_{环})$可得,物体的散热系数$k=\frac {q}{t_{物}-t_{环}}=\frac {q}{30^{\circ }C-20^{\circ }C}=\frac {q}{10^{\circ }C}$,当物体温度降低到$29^{\circ }C$时,散热快慢$q'=k(t_{物}'-t_{环})=\frac {q}{10^{\circ }C}×(29^{\circ }C-20^{\circ }C)=\frac {9}{10}q$.
(4)水从$30^{\circ }C$降到$25^{\circ }C$放出的热量$Q_{水放}=c_{水}m_{水}(t_{0水}-t_{水})=c_{水}ρ_{水}V_{水}×(30^{\circ }C-25^{\circ }C)=4.2×10^{3}J/(kg\cdot ^{\circ }C)×1×10^{3}kg/m^{3}×V_{水}×5^{\circ }C$ ①,盐水从$30^{\circ }C$降到$25^{\circ }C$放出的热量$Q_{盐水放}=c_{盐水}m_{盐水}(t_{0盐水}-t_{盐水})=c_{盐水}ρ_{盐水}V_{盐水}×(30^{\circ }C-25^{\circ }C)=c_{盐水}×1.1×10^{3}kg/m^{3}×V_{盐水}×5^{\circ }C$ ②,由题图乙可知,水和盐水的降温时间分别为24 min和22 min,故它们放出的热量之比$\frac {Q_{水放}}{Q_{盐水放}}=\frac {24min}{22min}=\frac {12}{11}$ ③,$V_{水}=V_{盐水}$,联立①②③,解得盐水的比热容$c_{盐水}=3.5×10^{3}J/(kg\cdot ^{\circ }C)$.
(1)热传递
(2)AC
(3)$\frac {9}{10}q$
(4)$3.5×10^{3}$ 解析:
(1)物体向周围环境散热,物体的内能转移到周围环境温度较低的物体上,内能减小,这种改变内能的方式是热传递.
(2)q是表示散热快慢的物理量,速度是表示物体运动快慢的物理量,功率是表示做功快慢的物理量,这三者的物理意义类似.
(3)当物体的温度为$30^{\circ }C$,周围环境温度为$20^{\circ }C$时,根据牛顿冷却定律$q=k(t_{物}-t_{环})$可得,物体的散热系数$k=\frac {q}{t_{物}-t_{环}}=\frac {q}{30^{\circ }C-20^{\circ }C}=\frac {q}{10^{\circ }C}$,当物体温度降低到$29^{\circ }C$时,散热快慢$q'=k(t_{物}'-t_{环})=\frac {q}{10^{\circ }C}×(29^{\circ }C-20^{\circ }C)=\frac {9}{10}q$.
(4)水从$30^{\circ }C$降到$25^{\circ }C$放出的热量$Q_{水放}=c_{水}m_{水}(t_{0水}-t_{水})=c_{水}ρ_{水}V_{水}×(30^{\circ }C-25^{\circ }C)=4.2×10^{3}J/(kg\cdot ^{\circ }C)×1×10^{3}kg/m^{3}×V_{水}×5^{\circ }C$ ①,盐水从$30^{\circ }C$降到$25^{\circ }C$放出的热量$Q_{盐水放}=c_{盐水}m_{盐水}(t_{0盐水}-t_{盐水})=c_{盐水}ρ_{盐水}V_{盐水}×(30^{\circ }C-25^{\circ }C)=c_{盐水}×1.1×10^{3}kg/m^{3}×V_{盐水}×5^{\circ }C$ ②,由题图乙可知,水和盐水的降温时间分别为24 min和22 min,故它们放出的热量之比$\frac {Q_{水放}}{Q_{盐水放}}=\frac {24min}{22min}=\frac {12}{11}$ ③,$V_{水}=V_{盐水}$,联立①②③,解得盐水的比热容$c_{盐水}=3.5×10^{3}J/(kg\cdot ^{\circ }C)$.
查看更多完整答案,请扫码查看


