《2025年名校课堂八年级数学上册人教版》

1. (2024·南充期末)下列各图中，$a$，$b$，$c$分别是三角形的边长，由甲、乙、丙三个三角形中标注的信息，能确定与$\triangle ABC$全等的是(C)


A.甲和乙
B.甲和丙
C.乙和丙
D.只有丙

答案： C

2. (2024·南充期末)如图，$\triangle ABC\cong\triangle DEC$，点$B$，$C$，$D$在同一条直线上，且$CE = 1$，$CD = 2$，则$AE$的长是____.

答案： 1

3. (2024·牡丹江)如图，在$\triangle ABC$中，$D$是$AB$上一点，$CF// AB$，$D$，$E$，$F$三点共线，请添加一个条件：________________________，使得$AE = CE$.（只添一种情况即可）

答案： DE=EF(答案不唯一)

4. (2024·南充嘉陵区期末)如图，在$\triangle ABC$中，$AB = 9$，$AC = 7$，$D$是边$BC$的中点，则$AD$的长$m$的取值范围为1＜m＜8.

答案： 1＜m＜8

5. (2024·南充期末)如图，在$Rt\triangle ABC$中，$\angle ACB = 90^{\circ}$，$Rt\triangle ABC$的角平分线$AD$，$BE$相交于点$O$，过点$O$作$OF\perp AD$，交$BC$的延长线于点$F$，交$AC$于点$G$，有下列结论：
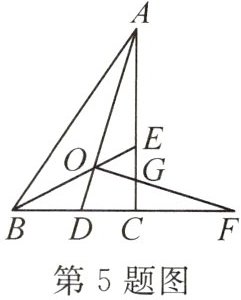
①$\angle AOB = 135^{\circ}$；②$BA = BF$；③$\triangle AOG\cong\triangle FOD$；④$BD + AG = AB$.其中正确的是①②③④.(填序号)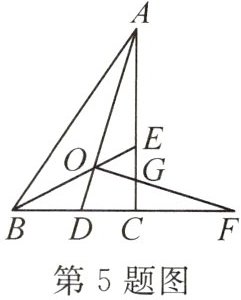

答案： ①②③④

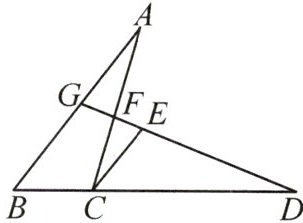
6. 如图，在$\triangle ABC$中，$D$是$BC$延长线上一点，满足$CD = AB$，过点$C$作$CE// AB$且$CE = BC$，连接$DE$并延长，分别交$AC$，$AB$于点$F$，$G$.
(1)求证：$\triangle ABC\cong\triangle DCE$.
(2)若$\angle B = 50^{\circ}$，$\angle D = 22^{\circ}$，求$\angle AFG$的度数.

答案： 6.解：
(1)证明：
∵CE//AB，
∴∠B=∠DCE.在△ABC和△DCE中，
$\begin{cases}$
∠ABC=∠DCE\\
BC=CE\\
∠ABC（此处原稿疑似遗漏条件，按常规推理应为BC等对应边相关，暂保留原稿形式）=（对应条件）
$\end{cases}（$此处原稿表述不太完整，按全等判定SAS应补充边对应关系，原稿为$\therefore\triangle ABC\cong\triangle DCE(SAS)），$
∵由
(1)知，$\triangle ABC\cong\triangle DCE，$$\begin{cases}BA=CD\\ \angle A = \angle D\\（$此处原稿疑似遗漏对应角或边关系，按后续推理补充思路应为边角相关$）\end{cases}，$$\therefore\triangle ECD（$应为$\triangle DCE$相关，原稿表述有误，按后续推理应为$\triangle DCE$中$）∠B = 50^{\circ}，$$\angle A=\angle D = 22^{\circ}。$
∵CE//AB，
∴$∠ACE=∠A = 22^{\circ}。$$∠CED = 180^{\circ}-\angle D-\angle ECD=108^{\circ}，$
∴$∠AFG = ∠DFC=∠CED - ∠ACE = 86^{\circ}。$

7. 新考向 真实情境 学习完全等三角形这章后，数学兴趣小组同学就“测量河两岸$A$，$B$两点间的距离”这一问题，设计了如下方案.

②测得$\angle DCB = 100^{\circ}$，$\angle ADC = 65^{\circ}$；
③在$CD$的延长线上取点$E$，使得$\angle BEC = 15^{\circ}$；
请根据以上方案求出$A$，$B$两点间的距离$AB$.

答案：
7.解：
∵$∠C = 100^{\circ}，$$∠ADC = 65^{\circ}，$
∴$∠CAD = 180^{\circ}-\angle C-\angle ADC = 15^{\circ}。$
∴∠CAD = ∠BEC。在△ACD和△ECB中，

∴△ACD≌△ECB(AAS)。
∴AC = CE。又
∵CB = CD，
∴AC - CB = CE - CD，即AB = DE = 30米。