第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
11. (2024·南充白塔中学月考)定义:若三角形中一个内角等于另一个内角的$2$倍,则称这个三角形为“倍角三角形”。已知$\triangle ABC$是“倍角三角形”,其中一个角为$30^{\circ}$,则$\triangle ABC$中最大角的度数为
90°或100°或135°
。
答案:
11.90°或100°或135°
12. 如图,这是可调节躺椅的示意图(数据如图),$AE$与$BD$的交点为$C$,且$\angle CAB$,$\angle CBA$,$\angle E$保持不变。为了舒适,需调整$\angle D$的大小,使$\angle EFD = 110^{\circ}$,则图中$\angle D$应
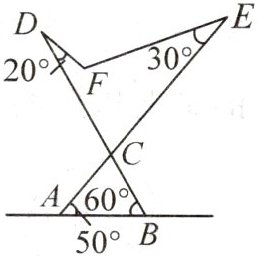
减少
(填“增加”或“减少”)10°
。(填度数)
答案:
12.减少 10°
13. (2024·泸州泸县期中)在$\triangle ABC$中,$\angle B$,$\angle C$均为锐角且不相等,线段$AD$是$\triangle ABC$中边$BC$上的高,$AE$是$\triangle ABC$的角平分线。
(1) 如图 1,若$\angle B = 70^{\circ}$,$\angle C = 30^{\circ}$,求$\angle DAE$的度数。
(2) 若$\angle B = x^{\circ}$,$\angle DAE = 10^{\circ}$,则$\angle C$的度数为
(3) 若$F$是射线$AE$上一动点,$G$,$H$分别为线段$AB$,$BC$上的点(不与端点重合),将$\triangle BGH$沿$GH$折叠,使点$B$落到点$F$处,如图 2 所示,请求出$\angle 1$,$\angle 2$与$\angle B$之间的数量关系。
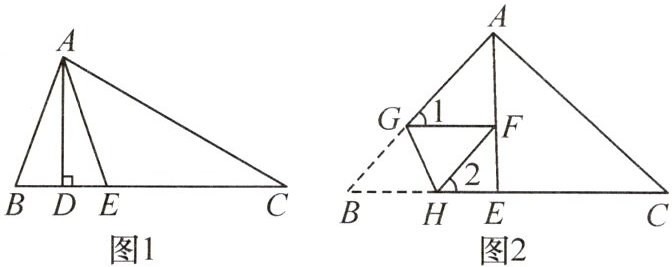
(1) 如图 1,若$\angle B = 70^{\circ}$,$\angle C = 30^{\circ}$,求$\angle DAE$的度数。
(2) 若$\angle B = x^{\circ}$,$\angle DAE = 10^{\circ}$,则$\angle C$的度数为
(x - 20)°或(x + 20)°
。(用含$x$的代数式表示)(3) 若$F$是射线$AE$上一动点,$G$,$H$分别为线段$AB$,$BC$上的点(不与端点重合),将$\triangle BGH$沿$GH$折叠,使点$B$落到点$F$处,如图 2 所示,请求出$\angle 1$,$\angle 2$与$\angle B$之间的数量关系。

答案:
13.解:
(1)在△ABC中,∠B = 70°,∠C = 30°,
∴∠BAC = 180° - ∠B - ∠C = 180° - 70° - 30° = 80°。
∵AE是△ABC的角平分线,
∴∠BAE = $\frac{1}{2}$∠BAC = $\frac{1}{2}$×80° = 40°。
∵线段AD是△ABC中边BC上的高,
∴∠ADB = 90°。
∴∠BAD = 180° - ∠B - ∠ADB = 180° - 70° - 90° = 20°。
∴∠DAE = ∠BAE - ∠BAD = 40° - 20° = 20°。
(2)(x - 20)°或(x + 20)°
(3)由折叠知,∠BGH = $\frac{1}{2}$∠BGF,∠BHG = $\frac{1}{2}$∠BHF。
∵∠BGF = 180° - ∠1,∠BHF = 180° - ∠2,
∴∠BGH = 90° - $\frac{1}{2}$∠1,∠BHG = 90° - $\frac{1}{2}$∠2。
∴∠B = 180° - ∠BGH - ∠BHG = $\frac{1}{2}$∠1 + $\frac{1}{2}$∠2,即∠1 + ∠2 = 2∠B。
(1)在△ABC中,∠B = 70°,∠C = 30°,
∴∠BAC = 180° - ∠B - ∠C = 180° - 70° - 30° = 80°。
∵AE是△ABC的角平分线,
∴∠BAE = $\frac{1}{2}$∠BAC = $\frac{1}{2}$×80° = 40°。
∵线段AD是△ABC中边BC上的高,
∴∠ADB = 90°。
∴∠BAD = 180° - ∠B - ∠ADB = 180° - 70° - 90° = 20°。
∴∠DAE = ∠BAE - ∠BAD = 40° - 20° = 20°。
(2)(x - 20)°或(x + 20)°
(3)由折叠知,∠BGH = $\frac{1}{2}$∠BGF,∠BHG = $\frac{1}{2}$∠BHF。
∵∠BGF = 180° - ∠1,∠BHF = 180° - ∠2,
∴∠BGH = 90° - $\frac{1}{2}$∠1,∠BHG = 90° - $\frac{1}{2}$∠2。
∴∠B = 180° - ∠BGH - ∠BHG = $\frac{1}{2}$∠1 + $\frac{1}{2}$∠2,即∠1 + ∠2 = 2∠B。
14. (2023·衢州)如图,这是脊柱侧弯的检测示意图,在体检时为方便测出 Cobb 角$\angle O$的大小,需将$\angle O$转化为与它相等的角,则图中与$\angle O$相等的角是(
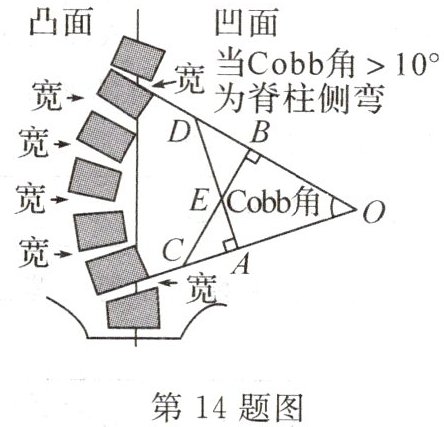
A.$\angle BEA$
B.$\angle DEB$
C.$\angle ECA$
D.$\angle ADO$
B
)
A.$\angle BEA$
B.$\angle DEB$
C.$\angle ECA$
D.$\angle ADO$
答案:
14.B
15. 新考向 跨学科 实践小组利用激光笔和平面镜演示平行光的反射实验。如图,一组平行光线$a$,$b$,$c$经过平面镜反射后得到一组互相平行的反射光线。若$\angle 1 = \angle 2 = 65^{\circ}$,则$\angle 3$的度数为

130°
。
答案:
15.130°
16. 新考向 数学文化 (2023·株洲)《周礼·考工记》中记载:“……半矩谓之宣(xuān),一宣有半谓之欘(zhú)……”意思是:“……直角的一半的角叫作宣,一宣半的角叫作欘……”($1$宣$= \frac{1}{2}$矩,$1$欘$= 1\frac{1}{2}$宣,$1$矩$= 90^{\circ}$)
问题:图 1 为中国古代一种强弩图,图 2 为这种强弩图的部分组件的示意图。若$\angle A = 1$矩,$\angle B = 1$欘,则$\angle C = $
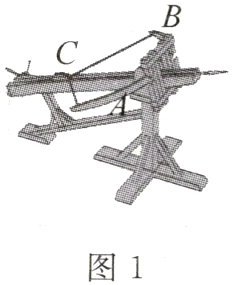
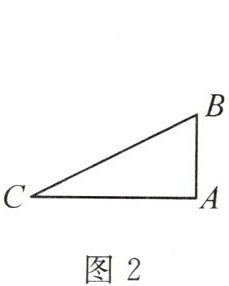
问题:图 1 为中国古代一种强弩图,图 2 为这种强弩图的部分组件的示意图。若$\angle A = 1$矩,$\angle B = 1$欘,则$\angle C = $
22.5°
。

答案:
16.22.5°
查看更多完整答案,请扫码查看


