第115页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
10. 某超市新进的一种砂糖橘很受客户欢迎.一客户第一次用$m$元购买了$n$千克,第二次购买时该砂糖橘的单价变成了第一次的$\frac{b}{a}$倍,则该客户第二次购买时砂糖橘的单价为 (
A.$\frac{m}{n}$
B.$\frac{mb}{na}$
C.$\frac{n}{m}$
D.$\frac{2mn}{ab}$
B
)A.$\frac{m}{n}$
B.$\frac{mb}{na}$
C.$\frac{n}{m}$
D.$\frac{2mn}{ab}$
答案:
B
11. 一条船往返于相距100 km的A,B两港之间,已知水流的速度是2 km/h,船在静水中的速度是$x$ km/h($x>2$),那么船在一次往返过程中,顺水航行的时间与逆水航行的时间比是
\frac{x - 2}{x + 2}
。
答案:
$11.\frac{x - 2}{x + 2}$
12. 若$\frac{x + 2}{x - 3}÷\frac{x + 1}{x - 2}$有意义,则$x$的取值范围是
x≠3且x≠2且x≠ - 1
。
答案:
12.x≠3且x≠2且x≠ - 1
13. 若$3a = 2b$,则$\frac{5a - b}{a^2 - 4b^2}\cdot(a - 2b)$的值是
\frac{7}{8}
。
答案:
$13.\frac{7}{8}$
14. 老师设计了接力游戏,用合作的方式完成分式化简,规则:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简.过程如图所示:
老师:$\frac{x^2 - 2x}{x - 1}\cdot\frac{x^2}{1 - x}$
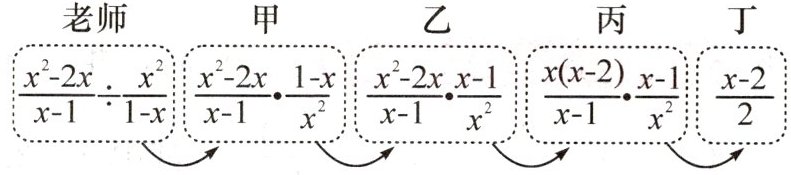
甲:$\frac{x^2 - 2x}{x - 1}\cdot\frac{1 - x}{x^2}$
乙:$\frac{x^2 - 2x}{x - 1}\cdot\frac{x - 1}{x^2}$
丙:$\frac{x(x - 2)}{x - 1}\cdot\frac{x - 1}{x^2}$
丁:$\frac{x - 2}{2}$
在接力中,自己负责的一步出现错误的是 (
A.只有乙
B.甲和丁
C.乙和丙
D.乙和丁
老师:$\frac{x^2 - 2x}{x - 1}\cdot\frac{x^2}{1 - x}$
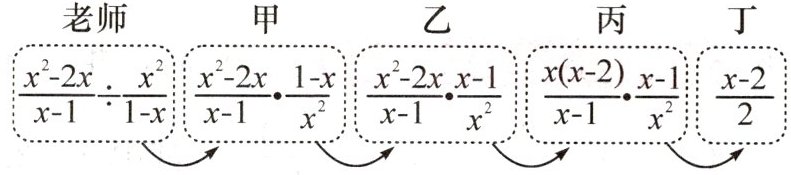
甲:$\frac{x^2 - 2x}{x - 1}\cdot\frac{1 - x}{x^2}$
乙:$\frac{x^2 - 2x}{x - 1}\cdot\frac{x - 1}{x^2}$
丙:$\frac{x(x - 2)}{x - 1}\cdot\frac{x - 1}{x^2}$
丁:$\frac{x - 2}{2}$
在接力中,自己负责的一步出现错误的是 (
D
)A.只有乙
B.甲和丁
C.乙和丙
D.乙和丁
答案:
D
15. 若化简$\frac{2}{x^2 - 1}÷\frac{1}{x - a}$的结果是$\frac{2}{x - 1}$,则$a$的值是 (
A.1
B.$-1$
C.2
D.$-2$
B
)A.1
B.$-1$
C.2
D.$-2$
答案:
B
16. 先化简:$\frac{x^2 + 4x + 4}{x^2 - 4}÷\frac{x^2 + 2x}{x - 2}$,然后在不等式$x\leq2$的非负整数解中选择一个合适的数代入求值。
答案:
16.解:原式$=\frac{(x + 2)²}{(x + 2)(x - 2)} · \frac{x - 2}{x(x + 2)} = \frac{1}{x}. $要使原式有意义,则x≠0,x≠±2.又
∵x≤2,且x为非负整数,
∴x只能取1.当x = 1时,原式=1.
∵x≤2,且x为非负整数,
∴x只能取1.当x = 1时,原式=1.
17. 有甲、乙两筐水果,甲筐水果重$(x - 1)^2$千克,乙筐水果重$(x^2 - 1)$千克(其中$x>1$),售完后,两筐水果都卖了50元。
(1)哪筐水果的单价更低?
(2)两筐水果中,高的单价是低的单价的多少倍?
(1)哪筐水果的单价更低?
(2)两筐水果中,高的单价是低的单价的多少倍?
答案:
17.解:
(1)甲筐水果的单价为$\frac{50}{(x - 1)²}$元,乙筐水果的单价为$\frac{50}{x² - 1}$元.
∵x > 1,
∴x² - 1 - (x - 1)² = x² - 1 - (x² - 2x + 1) = x² - 1 - x² + 2x - 1 = 2x - 2 = 2(x - 1) > 0.
∴0 < (x - 1)² < x² - 1.
∴$\frac{50}{x² - 1} < \frac{50}{(x - 1)²}.$答:乙筐水果的单价更低$.(2)\frac{50}{(x - 1)²} ÷ \frac{50}{x² - 1} = \frac{(x + 1)(x - 1)}{(x - 1)²} = \frac{x + 1}{x - 1}.$答:高的单价是低的单价的$\frac{x + 1}{x - 1}$倍.
(1)甲筐水果的单价为$\frac{50}{(x - 1)²}$元,乙筐水果的单价为$\frac{50}{x² - 1}$元.
∵x > 1,
∴x² - 1 - (x - 1)² = x² - 1 - (x² - 2x + 1) = x² - 1 - x² + 2x - 1 = 2x - 2 = 2(x - 1) > 0.
∴0 < (x - 1)² < x² - 1.
∴$\frac{50}{x² - 1} < \frac{50}{(x - 1)²}.$答:乙筐水果的单价更低$.(2)\frac{50}{(x - 1)²} ÷ \frac{50}{x² - 1} = \frac{(x + 1)(x - 1)}{(x - 1)²} = \frac{x + 1}{x - 1}.$答:高的单价是低的单价的$\frac{x + 1}{x - 1}$倍.
查看更多完整答案,请扫码查看


