第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
9. 如图,在△ABC中,AD平分∠BAC,BD=CD,则∠B与∠C相等吗?为什么?
解:相等. 理由如下:
∵AD平分∠BAC,
∴∠BAD=∠CAD.
在△ABD和△ACD中,
$\left\{\begin{array}{l}BD = CD, \\AD = AD, \\\angle BAD = \angle CAD,\end{array}\right.$
∴△ABD≌△ACD.
∴∠B=∠C.
以上解答是否正确?若不正确,请说明理由.
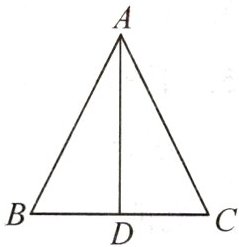
解:相等. 理由如下:
∵AD平分∠BAC,
∴∠BAD=∠CAD.
在△ABD和△ACD中,
$\left\{\begin{array}{l}BD = CD, \\AD = AD, \\\angle BAD = \angle CAD,\end{array}\right.$
∴△ABD≌△ACD.
∴∠B=∠C.
以上解答是否正确?若不正确,请说明理由.

答案:
解:不正确.理由:错用“SSA”来证明两个三角形全等,∠BAD不是BD与AD的夹角,∠CAD不是CD与AD的夹角.
10. 如图,已知∠AOB,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;再以点O为圆心,大于OC的长为半径画弧,分别交OA,OB于点E,F;连接CF,DE,CF与DE相交于点P,则下列结论错误的是(
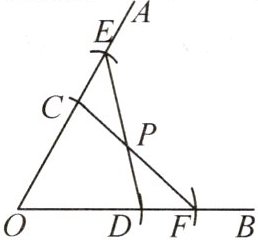
A.△EOD≌△FOC
B.∠CPE=∠CEP
C.CF=DE
D.∠OCF=∠ODE
B
)
A.△EOD≌△FOC
B.∠CPE=∠CEP
C.CF=DE
D.∠OCF=∠ODE
答案:
B
11. 【整体思想】如图,点C在线段BD上,∠B=∠D=40°,AB=CD,BC=DE,则∠ACE的度数是
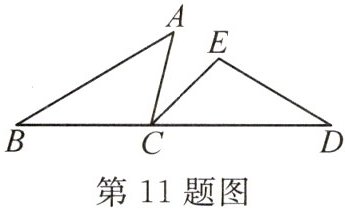
40°
.
答案:
40°
12. 茗茗用同种材料制成的金属框架如图所示,已知∠B=∠E,AB=DE,BF=EC,△ABC的周长为24 cm,CF=3 cm,则制成整个金属框架所需这种材料的长度为
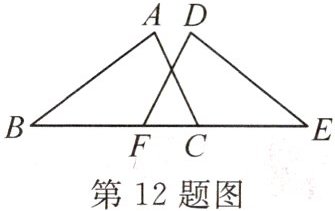
45
cm.
答案:
45
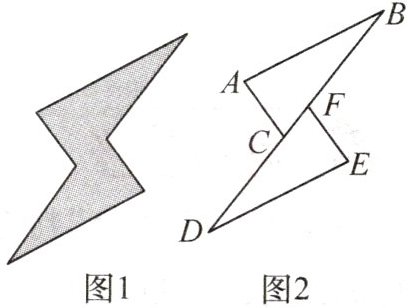
13. 图1是安全用电的标识图案,其中蕴含着几何知识. 如图2,点B,D,C,F在同一条直线上,且DC=BF,AB=ED,AB//ED.
(1)请判断AC与EF的数量关系和位置关系,并说明理由.
(2)若∠B=25°,∠E=75°,求∠ACB的度数.
(1)请判断AC与EF的数量关系和位置关系,并说明理由.
(2)若∠B=25°,∠E=75°,求∠ACB的度数.

答案:
解:
(1)AC = EF,AC//EF.理由如下:
∵AB//DE,
∴∠B = ∠D.DC = BF,
∴DC + CF = BF + CF,即DF = BC.在△ABC和△EDF中,$\begin{cases}AB = ED, \\ \angle B = \angle D, \\ BC = DF,\end{cases}$
∴△ABC≌△EDF(SAS).
∴AC = EF,∠ACB = ∠EFD.
∴AC//EF.
(2)由
(1),得△ABC≌△EDF,
∴∠A = ∠E = 75°.
∵∠A + ∠B + ∠ACB = 180°,∠B = 25°,
∴∠ACB = 180° - ∠A - ∠B = 80°.
(1)AC = EF,AC//EF.理由如下:
∵AB//DE,
∴∠B = ∠D.DC = BF,
∴DC + CF = BF + CF,即DF = BC.在△ABC和△EDF中,$\begin{cases}AB = ED, \\ \angle B = \angle D, \\ BC = DF,\end{cases}$
∴△ABC≌△EDF(SAS).
∴AC = EF,∠ACB = ∠EFD.
∴AC//EF.
(2)由
(1),得△ABC≌△EDF,
∴∠A = ∠E = 75°.
∵∠A + ∠B + ∠ACB = 180°,∠B = 25°,
∴∠ACB = 180° - ∠A - ∠B = 80°.
14. 如图,在△ABC中,AB=AC=24 cm,∠ABC=∠ACB,BC=16 cm,D为AB的中点. 点P在线段BC上以4 cm/s的速度由点B向点C运动,同时点Q在线段CA上以a cm/s的速度由点C向点A运动. 设运动的时间为t s.
(1)填空:
①BP=
②CQ=
(2)当a,t为何值时,以D,B,P为顶点的三角形和以P,C,Q为顶点的三角形全等?

(1)填空:
①BP=
4t
cm.②CQ=
at
cm.(用含t,a的代数式表示)(2)当a,t为何值时,以D,B,P为顶点的三角形和以P,C,Q为顶点的三角形全等?

答案:
解:
(1)①4t ②at
(2)由题意,得BD = $\frac{1}{2}$AB = 12cm,BP = 4t cm,CP = (16 - 4t)cm,CQ = at cm.
∵∠B = ∠C,分两种情况讨论:①当BD = CQ,BP = CP时,△DBP≌△QCP,
∴$\begin{cases}12 = at, \\4t = 16 - 4t,\end{cases}$ 解得$\begin{cases}a = 6, \\t = 2;\end{cases}$ ②当BD = CP,BP = CQ时,△DBP≌△PCQ,
∴$\begin{cases}12 = 16 - 4t, \\4t = at,\end{cases}$ 解得$\begin{cases}t = 1, \\a = 4.\end{cases}$综上所述,当a的值为6、t的值为2或a的值为4、t的值为1时,△DPB与△PCQ全等.
(1)①4t ②at
(2)由题意,得BD = $\frac{1}{2}$AB = 12cm,BP = 4t cm,CP = (16 - 4t)cm,CQ = at cm.
∵∠B = ∠C,分两种情况讨论:①当BD = CQ,BP = CP时,△DBP≌△QCP,
∴$\begin{cases}12 = at, \\4t = 16 - 4t,\end{cases}$ 解得$\begin{cases}a = 6, \\t = 2;\end{cases}$ ②当BD = CP,BP = CQ时,△DBP≌△PCQ,
∴$\begin{cases}12 = 16 - 4t, \\4t = at,\end{cases}$ 解得$\begin{cases}t = 1, \\a = 4.\end{cases}$综上所述,当a的值为6、t的值为2或a的值为4、t的值为1时,△DPB与△PCQ全等.
查看更多完整答案,请扫码查看


