《2025年名校课堂八年级数学上册人教版》

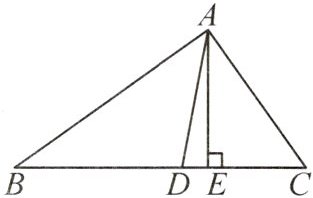
母题：A|清华附中校本经典题 如图，在△ABC 中，AD，AE 分别是△ABC 的角平分线和高线，∠ABC = α，∠ACB = β(α ＜ β).
(1)若α = 35°，β = 55°，则∠DAE = 10°.
(2)小明说：“无需给出α，β的具体数值，只需确定β与α的差值，即可确定∠DAE 的度数.”请通过计算验证小明的说法是否正确.

答案：
(1)$10^{\circ}$
(2)$\because \angle ABC=\alpha,\angle ACB=\beta.\therefore \angle BAC=180^{\circ}-\alpha-\beta.\therefore$AD平分$\angle BAC,\therefore \angle BAD=\frac{1}{2}\angle BAC=\frac{1}{2}(180^{\circ}-\alpha-\beta).\because AE\perp BC,\therefore$$\angle AEB=90^{\circ}.\therefore \angle BAE=90^{\circ}-\alpha.\therefore \angle DAE=\angle BAE-\angle BAD=(90^{\circ}-\alpha)$$-\frac{1}{2}(180^{\circ}-\alpha-\beta)=\frac{1}{2}(\beta-\alpha).\therefore \angle DAE$的度数与$\alpha,\beta$的具体数值无关，只和$\beta$与$\alpha$的差值有关。$\therefore$小明的说法是正确的。

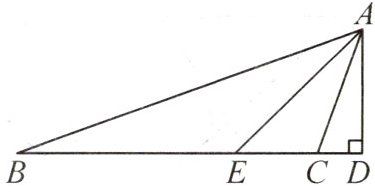
1. 如图，在△ABC 中，∠B = 20°，∠ACB = 110°，AE 平分∠BAC，AD⊥BD 于点 D，求∠DAE 的度数.

答案： 解：在$\triangle ABC$中，$\angle B=20^{\circ},\angle ACB=110^{\circ},\therefore \angle BAC=180^{\circ}-20^{\circ}-110^{\circ}$$=50^{\circ}.\because$AE平分$\angle BAC,\therefore \angle BAE=\frac{1}{2}\angle BAC=25^{\circ}.\therefore \angle AEC=\angle B$$+\angle BAE=20^{\circ}+25^{\circ}=45^{\circ}.\because AD\perp BD,\therefore \angle D=90^{\circ}.\therefore \angle DAE=90^{\circ}-\angle AED=90^{\circ}-45^{\circ}=45^{\circ}.$

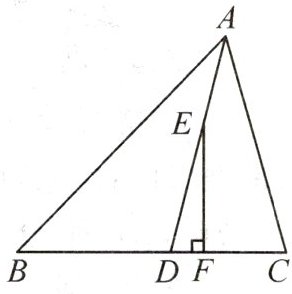
2. 如图，在△ABC 中，∠B ＜ ∠C，AD 平分∠BAC，E 为 AD(不与点 A，D 重合)上任意一点，EF⊥BC 于点 F. 若∠B = 46°，∠DEF = 14°，求∠C 的度数.

答案： 解：$\because EF\perp BC,\therefore \angle EFD=90^{\circ}.\therefore \angle EDF=90^{\circ}-\angle DEF=76^{\circ}.\because \angle B=$$46^{\circ},\therefore \angle BAD=\angle EDF-\angle B=30^{\circ}.\because AD$平分$\angle BAC,\therefore \angle BAC=$$2\angle BAD=2×30^{\circ}=60^{\circ}.\therefore \angle C=180^{\circ}-\angle B-\angle BAC=180^{\circ}-46^{\circ}-60^{\circ}$$=74^{\circ}.$

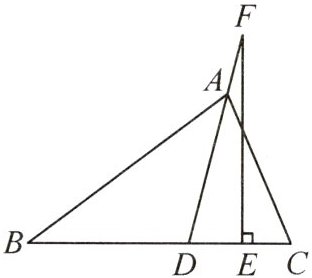
3. 如图，在△ABC 中，点 D，E 在边 BC 上，AD 平分∠BAC，F 为 DA 延长线上一点，FE⊥BC，∠B = 35°，∠C = 65°，则∠DFE 的度数为 15°.

答案： $15^{\circ}$

4. 如图，在△ABC 中，∠B ＞ ∠C，AE 平分∠BAC，在 AE 的延长线上任取一点 M，过点 M 作 MD⊥BC 于点 D，则∠M = $\frac{1}{2}$(∠B - ∠C)成立吗？试说明理由.

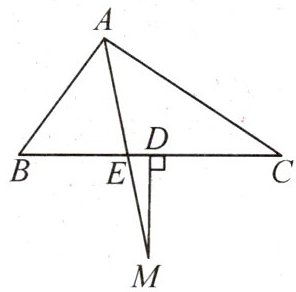
答案： 解：$\angle M=\frac{1}{2}(\angle B-\angle C)$成立.理由如下：过点A作$AN\perp BC$于点N.$\because \angle B+\angle C+\angle BAC=180^{\circ},\therefore \angle BAC=180^{\circ}-\angle B-\angle C.\because$AE平分$\angle BAC,\therefore \angle BAE=\frac{1}{2}\angle BAC=\frac{1}{2}(180^{\circ}-\angle B-\angle C)=90^{\circ}-\frac{1}{2}(\angle B$$+\angle C).\because AN\perp BC,\therefore \angle ANB=90^{\circ}.\therefore \angle BAN=90^{\circ}-\angle B.\therefore \angle NAE$$=\angle BAE-\angle BAN=90^{\circ}-\frac{1}{2}(\angle B+\angle C)-(90^{\circ}-\angle B)=\frac{1}{2}(\angle B-\angle C).\because \angle MDE=\angle ANE=90^{\circ},\therefore AN// DM.\therefore \angle M=\angle NAE=$$\frac{1}{2}(\angle B-\angle C).$