2025年智慧学堂八年级数学下册华师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年智慧学堂八年级数学下册华师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
9. 如图,在平行四边形ABCD中,M,N是BD上两点,BM = DN,连结AM,MC,CN,NA,添加一个条件,使四边形AMCN是矩形,这个条件是 ( )
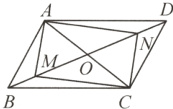
A. OM = $\frac{1}{2}$AC
B. MB = MO
C. BD⊥AC
D. ∠AMB = ∠CND

A. OM = $\frac{1}{2}$AC
B. MB = MO
C. BD⊥AC
D. ∠AMB = ∠CND
答案:
A
10.(雅安中考)如图,在△ABC中,∠C = 90°,AC = BC = 6,P为边AB上一动点,作PD⊥BC于点D,PE⊥AC于点E,则DE的最小值为________.


答案:
$3\sqrt{2}$
11.(雅安中考)如图,在△ABC中,D是BC的中点,E是AD的中点,过点A作AF//BC交CE的延长线于点F.
(1)求证:FA = BD;
(2)连结BF,若AB = AC,求证:四边形ADBF是矩形.

(1)求证:FA = BD;
(2)连结BF,若AB = AC,求证:四边形ADBF是矩形.

答案:
证明:
(1)
∵AF//BC,
∴∠AFE = ∠DCE,∠FAE = ∠CDE.又
∵E为AD的中点,AE = DE,
∴△AEF≌△DEC(A.A.S.),AF = DC.
(2)连接DF,
∵BD = CD,AF = DC,AF//DC,
∴四边形ADCF是平行四边形.
∵AB = AC,D为BC的中点,
∴AD⊥BC,即:在□ ADCF中,有一个角为直角,
∴□ ADCF是矩形.
(3)在Rt△ABD中,由勾股定理得:BD = $\sqrt{AB^{2}-AD^{2}}$=$\sqrt{5^{2}-4^{2}}$=3,S_{矩形ADCF}=DC×AD = 3×4 = 12,S_{△BCD}=$\frac{1}{2}$×6×4 = 6,S_{梯形ABCF}=S_{矩形ADCF}+S_{△BCD}=18.
(4)当点O运动到AC中点时,AO = CO.又
∵EO = FO,
∴四边形AECF是平行四边形.又
∵EC⊥EF,即有一个角为直角,
∴□ AECF是矩形.
(5)在Rt△CEF中,由勾股定理得:EF = $\sqrt{CE^{2}+CF^{2}}$=$\sqrt{12^{2}+5^{2}}$=13,
∵OE = OF,
∴OC = $\frac{1}{2}$EF = 6.5,S_{□ AECF}=EF×OC = 13×6.5 = 84.5
(1)
∵AF//BC,
∴∠AFE = ∠DCE,∠FAE = ∠CDE.又
∵E为AD的中点,AE = DE,
∴△AEF≌△DEC(A.A.S.),AF = DC.
(2)连接DF,
∵BD = CD,AF = DC,AF//DC,
∴四边形ADCF是平行四边形.
∵AB = AC,D为BC的中点,
∴AD⊥BC,即:在□ ADCF中,有一个角为直角,
∴□ ADCF是矩形.
(3)在Rt△ABD中,由勾股定理得:BD = $\sqrt{AB^{2}-AD^{2}}$=$\sqrt{5^{2}-4^{2}}$=3,S_{矩形ADCF}=DC×AD = 3×4 = 12,S_{△BCD}=$\frac{1}{2}$×6×4 = 6,S_{梯形ABCF}=S_{矩形ADCF}+S_{△BCD}=18.
(4)当点O运动到AC中点时,AO = CO.又
∵EO = FO,
∴四边形AECF是平行四边形.又
∵EC⊥EF,即有一个角为直角,
∴□ AECF是矩形.
(5)在Rt△CEF中,由勾股定理得:EF = $\sqrt{CE^{2}+CF^{2}}$=$\sqrt{12^{2}+5^{2}}$=13,
∵OE = OF,
∴OC = $\frac{1}{2}$EF = 6.5,S_{□ AECF}=EF×OC = 13×6.5 = 84.5
12.(云南中考)如图,在□ABCD中,连结BD,E为线段AD的中点,延长BE与CD的延长线交于点F,连结AF,∠BDF = 90°.
(1)求证:四边形ABDF是矩形;
(2)若AD = 5,DF = 3,求四边形ABCF的面积S.
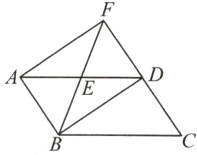
(1)求证:四边形ABDF是矩形;
(2)若AD = 5,DF = 3,求四边形ABCF的面积S.

答案:




13. 如图,在△ABC中,点O是边AC上一个动点,过点O作直线MN//BC. 设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE = OF;
(2)若CE = 12,CF = 5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.

(1)求证:OE = OF;
(2)若CE = 12,CF = 5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.

答案:
(1)证明:
∵CE,CF分别平分∠2,∠3,
∴∠4 + ∠6 = ∠5 + ∠6 = 90°.
(3)解:当点O在边AC上运动到AC的中点时,四边形AECF是矩形.理由:当点O为AC的中点时,AO = CO.又
∵EO = FO,
∴四边形AECF是平行四边形.又
∵∠ECF = 90°,
∴四边形AECF是矩形.
(1)证明:
∵CE,CF分别平分∠2,∠3,
∴∠4 + ∠6 = ∠5 + ∠6 = 90°.
(3)解:当点O在边AC上运动到AC的中点时,四边形AECF是矩形.理由:当点O为AC的中点时,AO = CO.又
∵EO = FO,
∴四边形AECF是平行四边形.又
∵∠ECF = 90°,
∴四边形AECF是矩形.
查看更多完整答案,请扫码查看


