《2025年智慧学堂八年级数学下册华师大版》

1. 如图，EF过矩形ABCD对角线的交点O且分别交AB，CD于点E，F，那么阴影部分的面积是矩形ABCD面积的（ ）

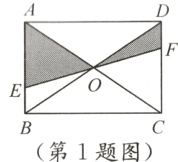
A. $\frac{1}{5}$
B. $\frac{1}{4}$
C. $\frac{1}{3}$
D. $\frac{3}{10}$

答案： B

2. 如图，将两块完全相同的矩形纸片ABCD和矩形纸片AEFG按图示方式放置（点A，D，E在同一直线上），连结AC，AF，CF，已知AD = 3，DC = 4，则CF的长是（ ）

A. 5
B. 7
C. 5$\sqrt{2}$
D. 10

答案： C

3.（市中区期末）如图，在矩形ABCD中，AB = 1，对角线AC与BD相交于点O，AE⊥BD，垂足为E. 若BE = EO，则AD的长是（ ）

A. 3$\sqrt{2}$
B. $\sqrt{3}$
C. 3$\sqrt{3}$
D. $\sqrt{5}$

答案： B

4.（青海中考）如图，在矩形ABCD中，对角线AC，BD相交于点O，已知∠BOC = 120°，DC = 3 cm，则AC的长为______ cm.

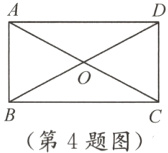
答案： 6

5. 如图，在矩形AOBC中，A（-2，0），B（0，1）. 若正比例函数y = kx的图象经过点C，则k的值为______.

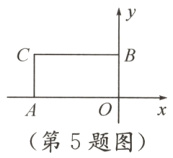
答案： $\frac{1}{2}$

6. 如图，在矩形ABCD中，M为CD中点，以B，M为圆心，分别以BC长，MC长为半径画弧，两弧相交于P点. 若∠PBC = 70°，则∠MPC的度数为______.

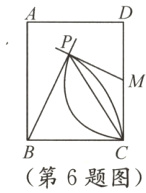
答案： $35^{\circ}$

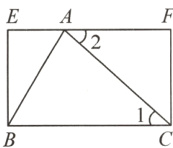
7.（重庆中考）我们知道，矩形的面积等于这个矩形的长乘宽，小明想用其验证一个底为a，高为h的三角形的面积公式为S = $\frac{1}{2}$ah. 想法是以BC为边作矩形BCFE，点A在边FE上，再过点A作BC的垂线，将其转化为证三角形全等，由全等图形面积相等来验证，按以上思路完成下面的作图与填空.
证明：过点A作BC的垂线AD交BC于点D.（要求：尺规作图并保留作图痕迹，不写作法，标明字母）
∵AD⊥BC，
∴∠ADC = 90°.
∵∠F = 90°，
∴∠ADC = ∠F.
∵EF//BC，
∴∠DAC = ∠FCA.
又∵AC = CA，
∴△ADC≌△CFA（A. A. S. ）.
同理可得，△ADB≌△BEA.
∴S_{△ABC}=S_{△ADC}+S_{△ABD}=$\frac{1}{2}$S_{矩形ADCF}+$\frac{1}{2}$S_{矩形AEBD}=$\frac{1}{2}$S_{矩形BCFE}=$\frac{1}{2}$ah.

答案： $\angle ADC=\angle F$；$\angle 1=\angle 2$；$AC = AC$；$\triangle ABD\cong\triangle BAE$

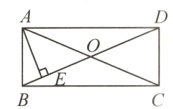
8. 如图，在矩形ABCD中，对角线AC，BD相交于点O，AE⊥BD，垂足为E，∠DAE：∠BAE = 3：1，那么∠EAC的度数是多少？

答案： 解：在矩形$ABCD$中，$\angle BAD = 90^{\circ}$，$OA = OD$，$\angle BAE:\angle EAD = 3:1$，$\therefore\angle BAE = 22.5^{\circ}$。$\because AE\perp BD$，易得$\angle ADO=\angle BAE = 22.5^{\circ}$。$\because OA = OD$，$\therefore\angle DAO=\angle ADO = 22.5^{\circ}$，$\therefore\angle EAC=\angle BAD-\angle BAE-\angle DAO = 45^{\circ}$。