《2025年诚成教育学业评价八年级数学下册人教版》

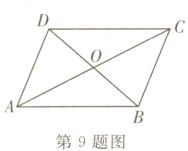
9. 如图，在平行四边形ABCD中，AC，BD相交于点O。下列结论：
①OA = OC；②∠BAD = ∠BCD；③AC⊥BD；④∠BAD + ∠ABC = 180°。其中结论正确的序号为( )

A. ①②
B. ②③
C. ①②④
D. ③④

答案： C

10. 计算:$(4\sqrt{2})^{2}=$______

答案： 32

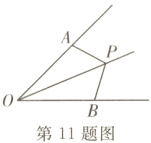
11. 如图所示，点P在∠AOB的平分线上，若使△AOP≌△BOP，则需添加的一个条件是__________(填一个即可)

答案： $OA = OB$等

12. 把$-\frac{1}{2}\sqrt{3}$的根号外面的因式移入根号内，结果是______

答案： $-\frac{1}{3}$

13. $\sqrt{3}+\sqrt{2}$的倒数是______

答案： $\sqrt{3}-\sqrt{2}$

14. 如图，在三角形纸片ABC中，∠C = 90°，∠A = 30°，AC = 3，折叠该纸片，使点A和点B重合，折痕与AB，AC分别交于点D和点E，折痕DE的长为______

答案： 1

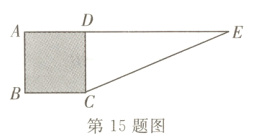
15. 如图，四边形ABCD为正方形，点A，D，E在同一条直线上，且DE = 12，CE = 13，则阴影部分的面积为______

答案： 25

16. 对于任意实数a，b，定义一种运算“△”如下：$a△b = a(a - b)+b(a + b)$，如$3△2 = 3(3 - 2)+2(3 + 2)=13$，则$\sqrt{3}△\sqrt{2}=$______

答案： 5

17. 新理念 多解题 在$\square ABCD$中，对角线AC，BD相交于点O，若AC = 14，BD = 8，AB = x，且x为大于8的整数，则AB的长是______

答案： 9或10

18. 新理念 规律题 观察规律：$\sqrt{3^{2}-1}=\sqrt{2}\times\sqrt{4}$，$\sqrt{4^{2}-1}=\sqrt{3}\times\sqrt{5}$，$\sqrt{5^{2}-1}=\sqrt{4}\times\sqrt{6}$，…。将你猜想到的规律用一个含n(n≥3且n为整数)的式子表示出来：________________

答案： $\sqrt{n^{2}-1}=\sqrt{n - 1}\cdot\sqrt{n + 1}$

19. (6分)计算:
(1) $\sqrt{2}(\sqrt{2}+\frac{1}{\sqrt{2}})-\frac{\sqrt{18}-\sqrt{8}}{\sqrt{2}}$；
(2) $(6\sqrt{\frac{x}{4}}-2x\sqrt{\frac{1}{x}})\div3\sqrt{x}$。

答案：
(1)2
(2)$\frac{1}{3}$