《2025年诚成教育学业评价八年级数学下册人教版》

23.(6分)有一块直角三角形绿地，量得两直角边长分别为6m,8m,现在要将绿地扩充成等腰三角形，且扩充部分是以原8m长的边为直角边的直角三角形，求扩充后等腰三角形绿地的周长.

答案：
解：记直角三角形绿地为$Rt\triangle ABC,\angle ACB = 90^{\circ},AC = 8\text{ m},BC = 6\text{ m}$.由勾股定理，得$AB = 10\text{ m}$，扩充部分为$Rt\triangle ACD$，扩充成等腰三角形$ABD$应分以下三种情况：
①如图①，当$AB = AD = 10\text{ m}$时，$CD = CB = 6\text{ m}$.所以$\triangle ABD$的周长为$32\text{ m}$；
②如图②，当$AB = BD = 10\text{ m}$时，由勾股定理，得$CD=\sqrt{BD^{2}-BC^{2}} = 4\sqrt{5}\text{ m}$.所以$\triangle ABD$的周长为$(20 + 4\sqrt{5})\text{ m}$；
③如图③，当$AB$为等腰三角形的底时，设$AD = BD = x\text{ m}$，则$CD=(x - 6)\text{ m}$，由勾股定理，得$(x - 6)^{2}+8^{2}=x^{2}$.解得$x=\frac{25}{3}$.所以$\triangle ABD$的周长为$\frac{80}{3}\text{ m}$.
综上，扩充后等腰三角形绿地的周长为$32\text{ m}$或$(20 + 4\sqrt{5})\text{ m}$或$\frac{80}{3}\text{ m}$.

24.(8分)如图，牧童在A处放羊，其家在B处，A，B到河岸的距离分别为AC = 400m，BD = 200m，CD = 800m，牧童从A处把羊牵到河边饮水后再回家.试问：在何处饮水，所走路程最短？最短路程是多少？
　　

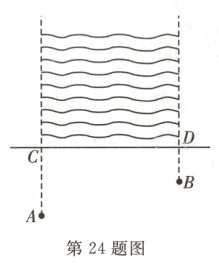
答案：
解：如图，作点$A$关于直线$CD$的对称点$G$，连接$BG$，交$CD$于点$E$，在点$E$处饮水，所走路程最短.
理由：$\because$点$A$与点$G$关于$CD$对称，$\therefore EA = EG$.
$\therefore AE + BE = GE + BE$
$\therefore$最短路程为$GB$的长.
过点$G$作$GH\perp BD$，交$BD$的延长线于点$H$.
$\because GH = CD = 800\text{ m}$，$BH = BD + DH = BD + GC = BD + AC = 200 + 400 = 600\text{ m}$，
$\therefore GB=\sqrt{GH^{2}+BH^{2}} = 1000\text{ m}$
即最短路程为$1000\text{ m}$.