《2025年诚成教育学业评价八年级数学下册人教版》

22. (5分)已知$m$是$\sqrt{2}$的小数部分，求$\sqrt{m^{2}+\frac{1}{m^{2}}-2}$的值。

答案： 2

23. 新理念 开放性试题(6分)实数$a$，$b$在数轴上的位置如图所示，化简$\sqrt{a^{2}-4a + 4}-(|a - b|-\sqrt{a^{2}}-\sqrt{b^{2}})$。写出一个满足条件的$a$值，并求出此时代数式的值。

答案： 解：由题意可知$a＜ - 2＜0＜b$，则$a - 2＜0$，$a - b＜0$.
原式$=\sqrt{(a - 2)^{2}}-(\vert a - b\vert-\vert a\vert-\vert b\vert)$
$=\vert a - 2\vert-(\vert a - b\vert-\vert a\vert-\vert b\vert)$
$=2 - a-(b - a + a - b)$
$=2 - a$.
当$a = - 2.5$时，原式$=4.5$(答案不唯一).

24. (7分)已知实数$a$，$b$在数轴上的对应点的位置如图所示，化简$\sqrt{a^{2}}+|a + b|+|\sqrt{2}-a|-\sqrt{(b - \sqrt{2})^{2}}$。

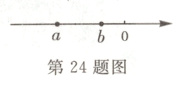
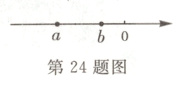
答案： 解：由数轴可知$a＜ - 2＜0＜b$，
$\therefore$原式$=\vert a\vert-\vert a - b\vert+\sqrt{a^{2}}-\sqrt{b^{2}}$
$=-a-(b - a)+(-a)-b$
$=-a - b + a - a - b$
$=-3a - 2b$
当$a$满足一定条件时结果为$-3a$.

25. 新理念 阅读理解试题(8分)已知$a$为实数，化简$\sqrt{-a^{3}}-a\sqrt{-\frac{1}{a}}$，阅读下面的解答过程，请判断是否正确，若不正确，请写出正确的解答过程。
解：$\sqrt{-a^{3}}-a\sqrt{-\frac{1}{a}}=a\cdot\sqrt{-a}-a\cdot\frac{1}{a}\sqrt{a}=(a - 1)\sqrt{a}$。

答案： 解：解答过程错误.
正确解答过程：
$\sqrt{-a^{3}}-a\sqrt{-\frac{1}{a}}$
$=-a\cdot\sqrt{-a}+a\cdot\frac{\sqrt{-a}}{a}$
$=(-a + 1)\sqrt{-a}$.

26. (9分)在比较同号两数的大小时，通常可以通过比较两个数的商与1的大小来判断这两个数的大小，如当$a$，$b$都是正数时，①若$\frac{a}{b}＞1$，则$a ＞ b$；②若$\frac{a}{b}=1$，则$a = b$；③若$\frac{a}{b}＜1$，则$a ＜ b$。我们将这种比较大小的方法叫做“作商法”。
(1) 请用上述方法比较$5\sqrt{7}$与$7\sqrt{5}$的大小；
(2) 写出$\frac{\sqrt{a}+1}{\sqrt{a}+2}$与$\frac{\sqrt{a}+2}{\sqrt{a}+3}$($a$为正整数)的大小关系，并证明你的结论。

答案： 解：
(1)$\because\frac{5\sqrt{7}}{7\sqrt{5}}=\sqrt{\frac{25\times7}{49\times5}}=\sqrt{\frac{5}{7}}＜1$，$\therefore5\sqrt{7}＜7\sqrt{5}$.
(2)$\frac{\sqrt{a}+1}{\sqrt{a}+2}＜\frac{\sqrt{a}+2}{\sqrt{a}+3}$.
证明：$\because\frac{\sqrt{a}+1}{\sqrt{a}+2}\div\frac{\sqrt{a}+2}{\sqrt{a}+3}$
$=\frac{\sqrt{a}+1}{\sqrt{a}+2}\cdot\frac{\sqrt{a}+3}{\sqrt{a}+2}$
$=\frac{a + 3 + 4\sqrt{a}}{a + 4 + 4\sqrt{a}}＜1$
$\therefore\frac{\sqrt{a}+1}{\sqrt{a}+2}＜\frac{\sqrt{a}+2}{\sqrt{a}+3}$.

27. 新理念 阅读理解试题(10分)小芳在解决问题“已知$a=\frac{1}{2+\sqrt{3}}$，求$2a^{2}-8a + 1$的值”时，是这样分析的：
$a=\frac{1}{2+\sqrt{3}}=\frac{2-\sqrt{3}}{(2+\sqrt{3})(2-\sqrt{3})}=2-\sqrt{3}$，
$\therefore(a - 2)^{2}=3$，即$a^{2}-4a + 4 = 3$。
$\therefore a^{2}-4a=-1$。
$\therefore2a^{2}-8a + 1=2(a^{2}-4a)+1=2\times(-1)+1=-1$。
(1) 化简：$\frac{1}{\sqrt{3}+1}+\frac{1}{\sqrt{5}+\sqrt{3}}+\frac{1}{\sqrt{7}+\sqrt{5}}+\cdots+\frac{1}{\sqrt{121}+\sqrt{119}}$；
(2) 若$a=\frac{1}{\sqrt{2}-1}$。
① 求$4a^{2}-8a - 1$的值；
② 求$3a^{3}-12a^{2}+9a - 12$的值。

答案： 解：
(1)原式$=\frac{\sqrt{3}-1+\sqrt{5}-\sqrt{3}+\sqrt{7}-\sqrt{5}+\cdots+\sqrt{121}-\sqrt{119}}{2}$
$=\frac{11 - 1}{2}=5$.
(2)①$\because a=\frac{1}{\sqrt{2}-1}=\sqrt{2}+1$，$\therefore$原式$=4(a - 1)^{2}-5=4\times(\sqrt{2}+1 - 1)^{2}-5=4\times2 - 5=3$.
②$\because a=\frac{1}{\sqrt{2}-1}=\sqrt{2}+1$，$\therefore a^{2}=3 + 2\sqrt{2}$. $\therefore$原式$=3a(a^{2}+3)-12(a^{2}+1)$