第103页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
27. (10分) 为了迎接“十一”长假的购物高峰,某运动品牌专卖店准备购进甲、乙两种运动鞋,其中甲、乙两种运动鞋的进价和售价如下表:
|运动鞋|甲|乙|
|--|--|--|
|进价/(元/双)|m|m - 20|
|售价/(元/双)|240|160|
已知用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1) 求m的值;
(2) 要使购进的甲、乙两种运动鞋共200双的总利润(利润 = 售价 - 进价)不少于21700元,且不超过22300元,问该专卖店有几种进货方案?
(3) 在(2)的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠a(50 < a < 70)元出售,乙种运动鞋价格不变,那么该专卖店要获得最大利润应如何进货?
|运动鞋|甲|乙|
|--|--|--|
|进价/(元/双)|m|m - 20|
|售价/(元/双)|240|160|
已知用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1) 求m的值;
(2) 要使购进的甲、乙两种运动鞋共200双的总利润(利润 = 售价 - 进价)不少于21700元,且不超过22300元,问该专卖店有几种进货方案?
(3) 在(2)的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠a(50 < a < 70)元出售,乙种运动鞋价格不变,那么该专卖店要获得最大利润应如何进货?
答案:
解:
(1)依题意得$\frac{3000}{m} = \frac{2400}{m - 20}$.
解得m = 100.
经检验m = 100是原分式方程的解,且符合题意.
所以m = 100.
(2)设购进甲种运动鞋x双,则购进乙种运动鞋(200 - x)双.
根据题意,得
$\begin{cases}(240 - 100)x + (160 - 80)(200 - x) \geq 21700①,\\(240 - 100)x + (160 - 80)(200 - x) \leq 22300②,\end{cases}$
解不等式①,得x ≥ 95.
解不等式②,得x ≤ 105.
所以不等式组的解集是95 ≤ x ≤ 105.
∵x是正整数,
∴共有11种进货方案.
(3)设总利润为W元,则
W = (240 - 100 - a)x + (160 - 80)(200 - x)
=(60 - a)x + 16000(95 ≤ x ≤ 105),
①当50 < a < 60时,
60 - a > 0,W随x的增大而增大,
所以当x = 105时,W有最大值,
此时应购进甲种运动鞋105双,乙种运动鞋95双;
②当a = 60时,
60 - a = 0,W = 16000,
(2)中所有方案获利都一样;
③当60 < a < 70时,60 - a < 0,
W随x的增大而减小.
所以当x = 95时,W有最大值,
此时应购进甲种运动鞋95双,乙种运动鞋105双.
(1)依题意得$\frac{3000}{m} = \frac{2400}{m - 20}$.
解得m = 100.
经检验m = 100是原分式方程的解,且符合题意.
所以m = 100.
(2)设购进甲种运动鞋x双,则购进乙种运动鞋(200 - x)双.
根据题意,得
$\begin{cases}(240 - 100)x + (160 - 80)(200 - x) \geq 21700①,\\(240 - 100)x + (160 - 80)(200 - x) \leq 22300②,\end{cases}$
解不等式①,得x ≥ 95.
解不等式②,得x ≤ 105.
所以不等式组的解集是95 ≤ x ≤ 105.
∵x是正整数,
∴共有11种进货方案.
(3)设总利润为W元,则
W = (240 - 100 - a)x + (160 - 80)(200 - x)
=(60 - a)x + 16000(95 ≤ x ≤ 105),
①当50 < a < 60时,
60 - a > 0,W随x的增大而增大,
所以当x = 105时,W有最大值,
此时应购进甲种运动鞋105双,乙种运动鞋95双;
②当a = 60时,
60 - a = 0,W = 16000,
(2)中所有方案获利都一样;
③当60 < a < 70时,60 - a < 0,
W随x的增大而减小.
所以当x = 95时,W有最大值,
此时应购进甲种运动鞋95双,乙种运动鞋105双.
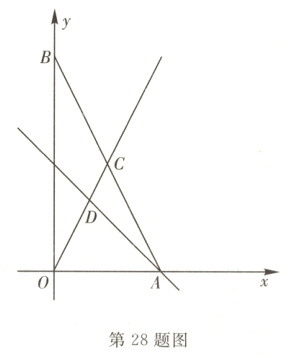
28. 新理念 综合探究题 (10分) 如图,在平面直角坐标系中,点A,B分别在x轴、y轴上,线段OA,OB的长(OA < OB)是方程组$\begin{cases}2x = y \\ 3x - y = 6\end{cases}$的解,C是直线y = 2x与直线AB的交点,点D在线段OC上,OD = 2$\sqrt{5}$.
(1) 求点C的坐标;
(2) 求直线AD的解析式;
(3) P是直线AD上的点,在平面内是否存在点Q,使以O,A,P,Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
(1) 求点C的坐标;
(2) 求直线AD的解析式;
(3) P是直线AD上的点,在平面内是否存在点Q,使以O,A,P,Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.

答案:
解:
(1)解方程组$\begin{cases}2x = y,\\3x - y = 6,\end{cases}$
得$\begin{cases}x = 6,\\y = 12.\end{cases}$
∵OA < OB,
∴OA = 6,OB = 12.
即A(6,0),B(0,12).
设直线AB的解析式为y = kx + b(k ≠ 0),
则$\begin{cases}6k + b = 0,\\b = 12,\end{cases}$
解得$\begin{cases}k = -2,\\b = 12.\end{cases}$
∴直线AB的解析式为y = -2x + 12.
联立$\begin{cases}y = -2x + 12,\\y = 2x,\end{cases}$
解得$\begin{cases}x = 3,\\y = 6.\end{cases}$
∴点C的坐标为(3,6).
(2)设点D的坐标为(a,2a),
∵OD = 2$\sqrt{5}$,
∴a² + (2a)² = (2$\sqrt{5}$)².
解得a = ± 2.
∵点D在线段OC上,
∴a = 2.
∴D(2,4).
设直线AD的解析式为y = mx + n(m ≠ 0),
把A(6,0),D(2,4)代入,
得$\begin{cases}6m + n = 0,\\2m + n = 4,\end{cases}$解得$\begin{cases}m = -1,\\n = 6.\end{cases}$
∴直线AD的解析式为y = -x + 6.
(3)存在. 点Q的坐标为(-3$\sqrt{2}$,3$\sqrt{2}$)或(3$\sqrt{2}$,-3$\sqrt{2}$)或(6,6)或(3,-3).
(1)解方程组$\begin{cases}2x = y,\\3x - y = 6,\end{cases}$
得$\begin{cases}x = 6,\\y = 12.\end{cases}$
∵OA < OB,
∴OA = 6,OB = 12.
即A(6,0),B(0,12).
设直线AB的解析式为y = kx + b(k ≠ 0),
则$\begin{cases}6k + b = 0,\\b = 12,\end{cases}$
解得$\begin{cases}k = -2,\\b = 12.\end{cases}$
∴直线AB的解析式为y = -2x + 12.
联立$\begin{cases}y = -2x + 12,\\y = 2x,\end{cases}$
解得$\begin{cases}x = 3,\\y = 6.\end{cases}$
∴点C的坐标为(3,6).
(2)设点D的坐标为(a,2a),
∵OD = 2$\sqrt{5}$,
∴a² + (2a)² = (2$\sqrt{5}$)².
解得a = ± 2.
∵点D在线段OC上,
∴a = 2.
∴D(2,4).
设直线AD的解析式为y = mx + n(m ≠ 0),
把A(6,0),D(2,4)代入,
得$\begin{cases}6m + n = 0,\\2m + n = 4,\end{cases}$解得$\begin{cases}m = -1,\\n = 6.\end{cases}$
∴直线AD的解析式为y = -x + 6.
(3)存在. 点Q的坐标为(-3$\sqrt{2}$,3$\sqrt{2}$)或(3$\sqrt{2}$,-3$\sqrt{2}$)或(6,6)或(3,-3).
查看更多完整答案,请扫码查看


