第101页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
24. (7分) 某市自来水公司为限制单位用水,每月只给某单位计划内用水3000吨,计划内用水每吨收费0.5元,超出计划部分每吨按0.8元收费.
(1) 写出该单位水费y(单位:元)与每月用水量x(单位:吨)之间的函数关系式:
① 用水量小于等于3000吨:____________;
② 用水量大于3000吨:____________;
(2) 某月该单位用水3200吨,水费是______元;若用水2800吨,水费是______元;
(3) 若某月该单位缴纳水费1540元,则该单位用水多少吨?
(1) 写出该单位水费y(单位:元)与每月用水量x(单位:吨)之间的函数关系式:
① 用水量小于等于3000吨:____________;
② 用水量大于3000吨:____________;
(2) 某月该单位用水3200吨,水费是______元;若用水2800吨,水费是______元;
(3) 若某月该单位缴纳水费1540元,则该单位用水多少吨?
答案:
解:
(1)①y = 0.5x.②y = 0.8x - 900.
(2)1660,1400.
(3)3050吨.
(1)①y = 0.5x.②y = 0.8x - 900.
(2)1660,1400.
(3)3050吨.
25. (8分) 甲、乙两车分别从A,B两地同时出发.甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地.设甲、乙两车距A地的路程为y(单位:千米),甲车行驶的时间为x(单位:小时),y与x之间的函数图象如图所示.
(1) 求甲车从A地到达B地的行驶时间;
(2) 求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围;
(3) 求乙车到达A地时,甲车距A地的路程.
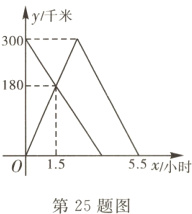
(1) 求甲车从A地到达B地的行驶时间;
(2) 求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围;
(3) 求乙车到达A地时,甲车距A地的路程.

答案:
解:
(1)300÷(180÷1.5) = 2.5(小时).
答:甲车从A地到达B地的行驶时间是2.5小时.
(2)设甲车返回时y与x之间的函数关系式为y = kx + b.
把点(2.5,300),(5.5,0)代入y = kx + b,
得$\begin{cases}2.5k + b = 300,\\5.5k + b = 0.\end{cases}$
解得$\begin{cases}k = -100,\\b = 550.\end{cases}$
∴甲车返回时y与x之间的函数关系式是y = -100x + 550(2.5 ≤ x ≤ 5.5).
(3)300÷[(300 - 180)÷1.5] = 3.75(小时).
当x = 3.75时,
y = -100×3.75 + 550 = 175.
答:乙车到达A地时,甲车距A地的路程是175千米.
(1)300÷(180÷1.5) = 2.5(小时).
答:甲车从A地到达B地的行驶时间是2.5小时.
(2)设甲车返回时y与x之间的函数关系式为y = kx + b.
把点(2.5,300),(5.5,0)代入y = kx + b,
得$\begin{cases}2.5k + b = 300,\\5.5k + b = 0.\end{cases}$
解得$\begin{cases}k = -100,\\b = 550.\end{cases}$
∴甲车返回时y与x之间的函数关系式是y = -100x + 550(2.5 ≤ x ≤ 5.5).
(3)300÷[(300 - 180)÷1.5] = 3.75(小时).
当x = 3.75时,
y = -100×3.75 + 550 = 175.
答:乙车到达A地时,甲车距A地的路程是175千米.
查看更多完整答案,请扫码查看


