《2026年成都中考真题精选物理》

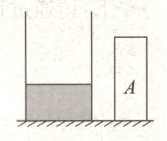
7. (6分)如图所示，一足够高的底面为正方形的薄壁容器放在水平桌面上，正方形的边长为10cm，容器内某液体的质量为2000g，液体的深度为10cm。实心圆柱体A的质量为600g，底面积为20cm²，高度为20cm且不吸水，g取10N/kg。
(1)求液体的密度；
(2)若将圆柱体A竖直放入容器内，请分析圆柱体A静止时所处的状态(请写出详细分析过程)，并算出此时圆柱体A受到的浮力大小；
(3)若在第(2)问的基础上将圆柱体A竖直向上提升1cm，求静止时液体对容器底部的压强p。

答案： 7.解:
(1)液体的质量为2000g,液体的深度为10cm,
体积V=S容h=10cm×10cm×10cm=1000cm³,
ρ=$\frac{m}{V}$=$\frac{2000g}{1000cm³}$=2g/cm³;
(2)圆柱体A的密度ρ'=$\frac{m'}{V'}$=$\frac{600g}{20cm×20cm²}$=1.5g/cm³,
圆柱体A的密度比液体密度小,当足够深时，圆柱体A可以漂浮，假设浸入的深度为h;
根据漂浮的条件知，浮力F浮=G=mg=0.6kg×10N/kg=6N,
根据阿基米德原理知，此时排开液体的体积
V排=$\frac{F浮}{ρg}$=$\frac{6N}{2.0×10³kg/m³×10N/kg}$=3×10⁻⁴m³=300cm³,
此时液体的深度
H=$\frac{V总}{S容}$=$\frac{1000cm³+300cm³}{10cm×10cm}$=13cm,
圆柱体A浸入的深度H'=$\frac{V排}{S_A}$=$\frac{300cm³}{20cm²}$=15cm,
液体深度小于物体浸入的深度，不能够漂浮;设此时液体的深度H'',则有10cm×10cm×H''=1000cm³+20cm²×H'',
解得H''=12.5cm=0.125m,
此时的浮力F浮=ρgV排=2.0×10³kg/m³×10N/kg×20×12.5×10⁻⁶m³=5N;
(3)在第
(2)问的基础上将圆柱体A竖直向上提升1cm,设液面下降的高度为h',
根据物体露出的体积等于液面降低的体积，则S_A(h'+h提)=S容h',
有20cm²×(1cm+h')=10cm×10cm×h',解得h'=0.25cm,
故静止时液体深度h''=H''−h'=12.5cm −0.25cm=12.25cm=0.1225m,
液体对容器底部的压强p=ρ液gh''=2.0×10³kg/m³×10N/kg×0.1225m=2.45×10³Pa。
答:
(1)液体的密度是2g/cm³;
(2)若将圆柱体A竖直放入容器内，圆柱体A静止时沉底，浮力为5N;
(3)若在第
(2)问的基础上将圆柱体A竖直向上提升1cm,求静止时液体对容器底部的压强p为2.45×10³Pa。
[考点]利用阿基米德原理进行简单计算;密度的简单计算;液体压强的公式及计算。