2025年学易优同步学案导学高中数学选择性必修第二册通用版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年学易优同步学案导学高中数学选择性必修第二册通用版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 已知数列 $\{ a_{n}\}$ 的首项 $a_{1}=1$,且满足 $a_{n + 1}=\dfrac {1}{2}a_{n}+\dfrac {1}{2n}$,则此数列的第 $3$ 项是(
A.$1$
B.$\dfrac {1}{2}$
C.$\dfrac {3}{4}$
D.$\dfrac {5}{8}$
C
)A.$1$
B.$\dfrac {1}{2}$
C.$\dfrac {3}{4}$
D.$\dfrac {5}{8}$
答案:
1.C $a_1=1$,$a_2=\frac{1}{2}a_1+\frac{1}{2}=1$,$a_3=\frac{1}{2}a_2+\frac{1}{2}×2=\frac{3}{4}$.
2. 已知数列 $\{ a_{n}\}$ 满足 $a_{n}=\dfrac {1}{a_{n - 1}}+1(n\geqslant 2,n\in \mathbf{N}^{*})$,若 $a_{4}=\dfrac {5}{3}$,则 $a_{1}$ 等于(
A.$1$
B.$\dfrac {3}{2}$
C.$2$
D.$\dfrac {8}{5}$
A
)A.$1$
B.$\dfrac {3}{2}$
C.$2$
D.$\dfrac {8}{5}$
答案:
2.A $\because a_4=\frac{5}{3}$,$a_4=\frac{1}{a_3}+1$,$\therefore a_3=\frac{3}{2}$,
又$\because a_3=\frac{1}{a_2}+1$,$\therefore a_2=2$,
又$\because a_2=\frac{1}{a_1}+1$,$\therefore a_1=1$.
又$\because a_3=\frac{1}{a_2}+1$,$\therefore a_2=2$,
又$\because a_2=\frac{1}{a_1}+1$,$\therefore a_1=1$.
3. 下列给出的图形中,星星的个数构成一个数列,则该数列的一个递推公式可以是(
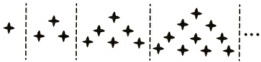
A.$a_{n + 1}=a_{n}+n$,$n\in \mathbf{N}^{*}$
B.$a_{n}=a_{n - 1}+n$,$n\in \mathbf{N}^{*}$,$n\geqslant 2$
C.$a_{n + 1}=a_{n}+(n + 1)$,$n\in \mathbf{N}^{*}$,$n\geqslant 2$
D.$a_{n}=a_{n - 1}+(n - 1)$,$n\in \mathbf{N}^{*}$,$n\geqslant 2$
B
)
A.$a_{n + 1}=a_{n}+n$,$n\in \mathbf{N}^{*}$
B.$a_{n}=a_{n - 1}+n$,$n\in \mathbf{N}^{*}$,$n\geqslant 2$
C.$a_{n + 1}=a_{n}+(n + 1)$,$n\in \mathbf{N}^{*}$,$n\geqslant 2$
D.$a_{n}=a_{n - 1}+(n - 1)$,$n\in \mathbf{N}^{*}$,$n\geqslant 2$
答案:
3.B 结合图象易知,$a_1=1$,$a_2=3=a_1+2$,$a_3=6=a_2+3$,$a_4=10=a_3+4$,
$\therefore a_n=a_{n - 1}+n$,$n\in N^*$,$n\geq2$.
$\therefore a_n=a_{n - 1}+n$,$n\in N^*$,$n\geq2$.
4. 在数列 $\{ a_{n}\}$ 中,$a_{1}=1$,$a_{2}=2$,$a_{n}+a_{n + 1}+a_{n + 2}=1$,$n\in \mathbf{N}^{*}$,则 $a_{2025}=$
-2
。
答案:
4.$-2$ $\because a_1=1$,$a_2=2$,$a_n+a_{n + 1}+a_{n + 2}=1$,
$\therefore a_3=1 - a_1 - a_2=1 - 1 - 2=-2$,
$a_4=1 - a_3 - a_2=1-(-2)-2=1$,
$a_5=1 - a_4 - a_3=1 - 1-(-2)=2$,
$·s$
依此类推,可得数列$\{a_n\}$是一个周期为$3$的周期
数列,
$\therefore a_{2025}=a_3=-2$.
$\therefore a_3=1 - a_1 - a_2=1 - 1 - 2=-2$,
$a_4=1 - a_3 - a_2=1-(-2)-2=1$,
$a_5=1 - a_4 - a_3=1 - 1-(-2)=2$,
$·s$
依此类推,可得数列$\{a_n\}$是一个周期为$3$的周期
数列,
$\therefore a_{2025}=a_3=-2$.
【问题1】 观察下面几个问题中的数列,回答下面的问题:
(1)近5届冬奥会举办的时间:2006,2010,2014,2018,2022;
(2)我国确定鞋号的脚长值以毫米为单位来表示,常用的中国鞋号按从大到小的顺序可排列为:45,44,43,42,41,40,⋯;
(3)为增强体质,学校增加了体育训练的项目,下面记录了某班内5名男生1分钟内引体向上的个数:10,10,10,10,10.
以上数列有什么共同特征?
(1)近5届冬奥会举办的时间:2006,2010,2014,2018,2022;
(2)我国确定鞋号的脚长值以毫米为单位来表示,常用的中国鞋号按从大到小的顺序可排列为:45,44,43,42,41,40,⋯;
(3)为增强体质,学校增加了体育训练的项目,下面记录了某班内5名男生1分钟内引体向上的个数:10,10,10,10,10.
以上数列有什么共同特征?
答案:
提示:对于
(1),我们发现2010-2006=4,2014-2010=4,2018-2014=4,2022-2018=4,也就是说该数列从第二项起,每一项与它的前一项的差都等于同一个常数。对于
(2)有44-45=-1,43-44=-1,…对于
(3),10-10=0,有同样的取值规律。
(1),我们发现2010-2006=4,2014-2010=4,2018-2014=4,2022-2018=4,也就是说该数列从第二项起,每一项与它的前一项的差都等于同一个常数。对于
(2)有44-45=-1,43-44=-1,…对于
(3),10-10=0,有同样的取值规律。
查看更多完整答案,请扫码查看


