《2025年学易优同步学案导学高中数学选择性必修第二册通用版》

【跟踪训练1】
(1)抛物线$y = \frac{1}{4}x^2$过点$(4,\frac{7}{4})$的切线方程为14x−4y−49=0或2x−4y−1 =0.
(2)求曲线$y = \frac{1}{x}$在点$(2,\frac{1}{2})$处的切线方程.

答案：
(1)14x−4y−49=0或2x−4y−1 =0　设过点(4,$\frac{7}{4}$)的切线与抛物线相切于点(x₀,$\frac{1}{4}$x₀²),
∵f'(x₀)=lim$_{\Delta x \to 0}$$\frac{\frac{1}{4}(x_0+\Delta x)^2-\frac{1}{4}x_0^2}{\Delta x}$
　=lim$_{\Delta x \to 0}$($\frac{1}{2}$x₀+$\frac{1}{4}$$\Delta x$)=$\frac{1}{2}$x₀,
∴$\frac{\frac{1}{4}x_0^2-\frac{7}{4}}{x_0-4}$=$\frac{1}{2}$x₀,
　即x₀²−8x₀+7=0,
　解得x₀=7或x₀=1,
　即切点坐标为(7,$\frac{49}{4}$),(1,$\frac{1}{4}$),
　故切线方程为y−$\frac{49}{4}$=$\frac{7}{2}$(x−7)或y−$\frac{1}{4}$=$\frac{1}{2}$(x −1),
　化简得14x−4y−49=0或2x−4y−1=0,即所求的切线方程为
　14x−4y−49=0或2x−4y−1=0.
(2)解:曲线在点(2,$\frac{1}{2}$)处的切线的斜率为k=lim$_{\Delta x \to 0}$$\frac{\frac{1}{2+\Delta x}-\frac{1}{2}}{\Delta x}$=lim$_{\Delta x \to 0}$$\frac{-1}{2(2+\Delta x)}$=−$\frac{1}{4}$,
　由直线的点斜式方程可得切线方程为
　y−$\frac{1}{2}$=−$\frac{1}{4}$(x−2),即x+4y−4=0.

【问题2】 函数的单调性和导数有什么关系?

答案：
提示:如图
　　　　　　
当t=t₀时，函数的图象在t=t₀处的切线平行于t轴,即h'(t₀)=0,这时，在t=t₀附近曲线比较平坦，几乎没有升降.
当t=t₁时，函数的图象在t=t₁处的切线l₁的斜率h'(t₁)＜0,这时，在t=t₁附近曲线下降，即函数在t=t₁附近单调递减.
当t=t₂时，函数的图象在t=t₂处的切线l₂的斜率h'(t₂)＜0,这时,在t=t₂附近曲线下降，即函数在t=t₂附近单调递减.
通过研究t=t₁和t=t₂发现直线l₁的倾斜程度小于直线l₂的倾斜程度，这说明函数在t=t₁附近比在t=t₂附近下降得缓慢.

若$f^{\prime}(x_0)=0$，则函数在$x = x_0$处切线斜率$k =$0.
若$f^{\prime}(x_0)＞0$，则函数在$x = x_0$处切线斜率$k$＞0，且函数在$x = x_0$附近单调递增，且$f^{\prime}(x_0)$越大，说明函数图象变化得越快.
若$f^{\prime}(x_0)＜0$，则函数在$x = x_0$处切线斜率$k$＜0，且函数在$x = x_0$附近单调递减，且$\vert f^{\prime}(x_0)\vert$越大，说明函数图象变化得越快.

答案： 0　＞　单调递增　＜　单调递减

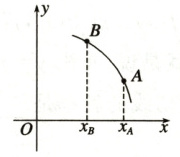
【例2】 已知$y = f(x)$的图象如图所示，则$f^{\prime}(x_A)$与$f^{\prime}(x_B)$的大小关系是 (B)


A.$f^{\prime}(x_A)＞f^{\prime}(x_B)$
B.$f^{\prime}(x_A)＜f^{\prime}(x_B)$
C.$f^{\prime}(x_A)=f^{\prime}(x_B)$
D.不能确定

答案： B　由导数的几何意义,f'(xₐ)，f'(x_b)分别是切线在点A，B处切线的斜率，由图象可知f'(xₐ)＜f'(x_b).