2025年学易优同步学案导学高中数学选择性必修第二册通用版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年学易优同步学案导学高中数学选择性必修第二册通用版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
【例3】 如图所示,作边长为$a$的正三角形的内切圆,在这个圆内作内接正三角形,然后再作新三角形的内切圆. 如此下去,前$n$个内切圆的面积和为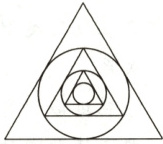
【总结导通】此类几何问题可以转化为等比数列模型,利用等比数列的有关知识解决,要注意步骤的规范性.
$\frac{a^{2}}{9}(1 - \frac{1}{2^{2n}})\pi$
.
【总结导通】此类几何问题可以转化为等比数列模型,利用等比数列的有关知识解决,要注意步骤的规范性.
答案:
$\frac{a^{2}}{9}(1 - \frac{1}{2^{2n}})\pi$ 设第$n$个正三角形的内切
圆的半径为$a_{n}$,
∵从第二个正三角形开始每一个正三角形的边
长是前一个的$\frac{1}{2}$,
每一个正三角形的内切圆半径也是前一个正三
角形内切圆半径的$\frac{1}{2}$,
∴$a_{1} = \frac{1}{2}a\tan 30^{\circ} = \frac{\sqrt{3}}{6}a$,$a_{2} = \frac{1}{2}a_{1}$,…,$a_{n} = \frac{1}{2}a_{n - 1}$,
∴数列$\{a_{n}\}$是以$\frac{\sqrt{3}}{6}a$为首项,$\frac{1}{2}$为公比的等比数列,
∴$a_{n} = \frac{\sqrt{3}}{6} × (\frac{1}{2})^{n - 1}a$,
设前$n$个内切圆的面积和为$S_{n}$,
则$S_{n} = \pi(a_{1}^{2} + a_{2}^{2} + … + a_{n}^{2})$
$ = \pi a^{2}[1 + (\frac{1}{2})^{2} + (\frac{1}{4})^{2} + … + (\frac{1}{2^{n - 1}})^{2}]$
$ = \pi a^{2}[1 + \frac{1}{4} + (\frac{1}{4})^{2} + … + (\frac{1}{4})^{n - 1}]$
$ = \frac{4}{3} × \frac{a^{2}}{12}(1 - \frac{1}{4^{n}})\pi = \frac{a^{2}}{9}(1 - \frac{1}{4^{n}})\pi$
$ = \frac{a^{2}}{9}(1 - \frac{1}{2^{2n}})\pi$.
圆的半径为$a_{n}$,
∵从第二个正三角形开始每一个正三角形的边
长是前一个的$\frac{1}{2}$,
每一个正三角形的内切圆半径也是前一个正三
角形内切圆半径的$\frac{1}{2}$,
∴$a_{1} = \frac{1}{2}a\tan 30^{\circ} = \frac{\sqrt{3}}{6}a$,$a_{2} = \frac{1}{2}a_{1}$,…,$a_{n} = \frac{1}{2}a_{n - 1}$,
∴数列$\{a_{n}\}$是以$\frac{\sqrt{3}}{6}a$为首项,$\frac{1}{2}$为公比的等比数列,
∴$a_{n} = \frac{\sqrt{3}}{6} × (\frac{1}{2})^{n - 1}a$,
设前$n$个内切圆的面积和为$S_{n}$,
则$S_{n} = \pi(a_{1}^{2} + a_{2}^{2} + … + a_{n}^{2})$
$ = \pi a^{2}[1 + (\frac{1}{2})^{2} + (\frac{1}{4})^{2} + … + (\frac{1}{2^{n - 1}})^{2}]$
$ = \pi a^{2}[1 + \frac{1}{4} + (\frac{1}{4})^{2} + … + (\frac{1}{4})^{n - 1}]$
$ = \frac{4}{3} × \frac{a^{2}}{12}(1 - \frac{1}{4^{n}})\pi = \frac{a^{2}}{9}(1 - \frac{1}{4^{n}})\pi$
$ = \frac{a^{2}}{9}(1 - \frac{1}{2^{2n}})\pi$.
【跟踪训练3】 如图,正三角形$ABC$的边长为20 cm,取BC边的中点E,作正三角形BDE;取DE边的中点G,作正三角形DFG……,如此继续下去,可得到一列三角形$\triangle ABC, \triangle BDE$,$\triangle DFG ·s$,则前20个正三角形的面积和为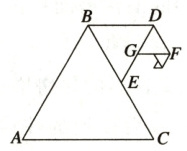
$\frac{400\sqrt{3}}{3}(1 - \frac{1}{4^{20}}) cm^2$
.
答案:
$\frac{400\sqrt{3}}{3}(1 - \frac{1}{4^{20}}) cm^2$ 设第$n$个
三角形边长为$a$,则第$n + 1$个三角形边长为$\frac{a}{2}$,
设第$n$个三角形面积为$a_{n}$,则$a_{n} = \frac{\sqrt{3}}{4}a^{2}$,$a_{n + 1} = \frac{\sqrt{3}}{4} · (\frac{a}{2})^{2} = \frac{\sqrt{3}}{16}a^{2}$,
∴$\frac{a_{n + 1}}{a_{n}} = \frac{1}{4}$,$a_{1} = S_{\triangle ABC} = \frac{\sqrt{3}}{4} × 20^{2} = 100\sqrt{3}$,
所以这些三角形面积成等比数列,且公比$q = \frac{1}{4}$,
首项$a_{1} = 100\sqrt{3}$,
所以前$20$个正三角形的面积和为
$S_{20} = \frac{100\sqrt{3}(1 - \frac{1}{4^{20}})}{1 - \frac{1}{4}} = \frac{400\sqrt{3}}{3}(1 - \frac{1}{4^{20}})( cm^2)$.
三角形边长为$a$,则第$n + 1$个三角形边长为$\frac{a}{2}$,
设第$n$个三角形面积为$a_{n}$,则$a_{n} = \frac{\sqrt{3}}{4}a^{2}$,$a_{n + 1} = \frac{\sqrt{3}}{4} · (\frac{a}{2})^{2} = \frac{\sqrt{3}}{16}a^{2}$,
∴$\frac{a_{n + 1}}{a_{n}} = \frac{1}{4}$,$a_{1} = S_{\triangle ABC} = \frac{\sqrt{3}}{4} × 20^{2} = 100\sqrt{3}$,
所以这些三角形面积成等比数列,且公比$q = \frac{1}{4}$,
首项$a_{1} = 100\sqrt{3}$,
所以前$20$个正三角形的面积和为
$S_{20} = \frac{100\sqrt{3}(1 - \frac{1}{4^{20}})}{1 - \frac{1}{4}} = \frac{400\sqrt{3}}{3}(1 - \frac{1}{4^{20}})( cm^2)$.
1. 某森林原有木材量为$a m^3$,每年以25%的速度增长,5年后,这片森林共有木材量
(
A.$a(1 + 25\%)^5$
B.$a(1 + 25\%)^4$
C.$4a\left[ \left( \frac{5}{4} \right)^5 - 1\right]$
D.$a(1 + 25\%)^6$
(
A
)A.$a(1 + 25\%)^5$
B.$a(1 + 25\%)^4$
C.$4a\left[ \left( \frac{5}{4} \right)^5 - 1\right]$
D.$a(1 + 25\%)^6$
答案:
1.A 森林中原有木材量为$a$,一年后为$a(1 + 25\%)$,两年后为$a(1 + 25\%)^{2}$,…,五年后为$a(1 + 25\%)^{5}$.
2. 观察一列算式:$1 \otimes 1, 1 \otimes 2, 2 \otimes 1, 1 \otimes 3, 2 \otimes 2, 3 \otimes 1, 1 \otimes 4, 2 \otimes 3, 3 \otimes 2, 4 \otimes 1, ·s$,则式子$3 \otimes 5$是第 (
A.22 项
B.23 项
C.24 项
D.25 项
C
)A.22 项
B.23 项
C.24 项
D.25 项
答案:
2.C 两数和为$2$的有$1$个,和为$3$的有$2$个,和为$4$的有$3$个,和为$5$的有$4$个,和为$6$的有$5$个,
和为$7$的有$6$个,前面共有$21$个,$3\otimes5$为和为$8$的第$3$项,故$3\otimes5$是第$24$项.
和为$7$的有$6$个,前面共有$21$个,$3\otimes5$为和为$8$的第$3$项,故$3\otimes5$是第$24$项.
3. 公元前5世纪,古希腊哲学家芝诺发表了著名的阿基里斯悖论:他提出让乌龟在阿基里斯前面1 000米处和阿基里斯赛跑,并且假定阿基里斯的速度是乌龟的10倍. 当比赛开始后,若阿基里斯跑了1 000米,此时乌龟便领先他100米;当阿基里斯跑完下一个100米时,乌龟仍然领先他1米……,所以,阿基里斯永远追不上乌龟. 按照这样的规律,若阿基里斯和乌龟的距离恰好为$10^{-2}$米时,乌龟爬行的总距离为 (
A.$\frac{10^4 - 1}{90}$米
B.$\frac{10^5 - 1}{900}$米
C.$\frac{10^5 - 9}{90}$米
D.$\frac{10^4 - 9}{900}$米
B
)A.$\frac{10^4 - 1}{90}$米
B.$\frac{10^5 - 1}{900}$米
C.$\frac{10^5 - 9}{90}$米
D.$\frac{10^4 - 9}{900}$米
答案:
3.B 由题意知,乌龟每次爬行的距离构成等比数
列$\{a_{n}\}$,且$a_{1} = 100$,$q = \frac{1}{10}$,$a_{n} = 10^{- 2}$;
∴乌龟爬行的总距离为$S_{n} = \frac{a_{1} - a_{n}q}{1 - q} = \frac{100 - 10^{- 2} × \frac{1}{10}}{1 - \frac{1}{10}} = \frac{10^{5} - 1}{900}$(米).
列$\{a_{n}\}$,且$a_{1} = 100$,$q = \frac{1}{10}$,$a_{n} = 10^{- 2}$;
∴乌龟爬行的总距离为$S_{n} = \frac{a_{1} - a_{n}q}{1 - q} = \frac{100 - 10^{- 2} × \frac{1}{10}}{1 - \frac{1}{10}} = \frac{10^{5} - 1}{900}$(米).
4. 中国三大名楼之一的黄鹤楼因其独特的建筑结构而闻名,其外观有五层而实际上内部有九层,隐喻“九五至尊”之意,现打算在黄鹤楼内部挂灯笼进行装饰,若在黄鹤楼内部九层塔楼共挂1533盏灯笼,且相邻的两层中,下一层的灯笼数是上一层灯笼数的两倍,则内部塔楼的顶层应挂
3
盏灯笼.
答案:
4.3 依题意,各层灯笼数从上到下排成一列构成
等比数列$\{a_{n}\}(n \in N^{*},n \leq 9)$,公比$q = 2$,前$9$项
和为$1533$,于是得$S_{9} = \frac{a_{1}(1 - 2^{9})}{1 - 2} = 1533$,解得
$a_{1} = 3$,所以内部塔楼的顶层应挂$3$盏灯笼.
等比数列$\{a_{n}\}(n \in N^{*},n \leq 9)$,公比$q = 2$,前$9$项
和为$1533$,于是得$S_{9} = \frac{a_{1}(1 - 2^{9})}{1 - 2} = 1533$,解得
$a_{1} = 3$,所以内部塔楼的顶层应挂$3$盏灯笼.
查看更多完整答案,请扫码查看


