2025年学易优同步学案导学高中数学选择性必修第二册通用版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年学易优同步学案导学高中数学选择性必修第二册通用版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第85页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 下列所给函数为复合函数的是 (
A.$y=\ln(x - 2)$
B.$y=\ln x+x - 2$
C.$y=(x - 2)\ln x$
D.$y=\frac{\ln x}{x - 2}$
A
)A.$y=\ln(x - 2)$
B.$y=\ln x+x - 2$
C.$y=(x - 2)\ln x$
D.$y=\frac{\ln x}{x - 2}$
答案:
1.A 函数$y = \ln(x - 2)$是由函数$y = \ln u$和$u = \varphi(x) = x - 2$复合而成的,而B、C、D中的函数分别为函数$y = \ln x$与函数$\varphi(x) = x - 2$的加、乘、商的形式,不符合复合函数的定义,选A.
2. 设$f(x)=\log_3(x - 1)$,则$f'(2)$等于(
A.$\ln 3$
B.$-\ln 3$
C.$\frac{1}{\ln 3}$
D.$-\frac{1}{\ln 3}$
C
)A.$\ln 3$
B.$-\ln 3$
C.$\frac{1}{\ln 3}$
D.$-\frac{1}{\ln 3}$
答案:
2.C $f'(x) = \frac{1}{(x - 1)\ln 3}$,故$f'(2) = \frac{1}{\ln 3}$.
3. 函数$y = x\ln(2x + 5)$的导数为 (
A.$\ln(2x + 5)-\frac{x}{2x + 5}$
B.$\ln(2x + 5)+\frac{2x}{2x + 5}$
C.$2x\ln(2x + 5)$
D.$\frac{x}{2x + 5}$
B
)A.$\ln(2x + 5)-\frac{x}{2x + 5}$
B.$\ln(2x + 5)+\frac{2x}{2x + 5}$
C.$2x\ln(2x + 5)$
D.$\frac{x}{2x + 5}$
答案:
3.B $\because y = x\ln(2x + 5)$,
$\therefore y' = \ln(2x + 5) + \frac{2x}{2x + 5}$.
$\therefore y' = \ln(2x + 5) + \frac{2x}{2x + 5}$.
4. 曲线$y = \sin^2x$在点$A(\frac{\pi}{6},\frac{1}{4})$处的切线的斜率是
$\frac{\sqrt{3}}{2}$
.
答案:
4.$\frac{\sqrt{3}}{2}$ $\because y' = (\sin^2 x)' = 2\sin x(\sin x)' = 2\sin x\cos x = \sin 2x$,
$\therefore y'|_{x = \frac{\pi}{6}} = \sin\frac{\pi}{3} = \frac{\sqrt{3}}{2}$,
$\therefore$曲线在点$A(\frac{\pi}{6},\frac{1}{4})$处的切线的斜率为$\frac{\sqrt{3}}{2}$.
$\therefore y'|_{x = \frac{\pi}{6}} = \sin\frac{\pi}{3} = \frac{\sqrt{3}}{2}$,
$\therefore$曲线在点$A(\frac{\pi}{6},\frac{1}{4})$处的切线的斜率为$\frac{\sqrt{3}}{2}$.
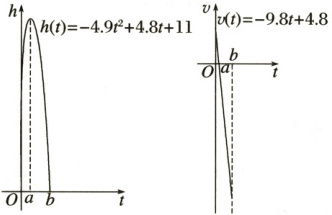
【问题1】 观察下面高台跳水的运动轨迹以及其导数的图象,试说明运动员从起跳到最高点,以及从最高点到入水这两段时间的运动状态有什么区别?如何从数学上刻画这种区别?
$h(t)=-4.9t^{2}+4.8t+11$,$v(t)=-9.8t+4.8$
$h(t)=-4.9t^{2}+4.8t+11$,$v(t)=-9.8t+4.8$

答案:
提示:通过观察图象,可以发现
(1)运动员从起跳到最高点,离水面的高度h随时间t的增加而增加,即h(t)单调递增,相应地,v(t)=h'(t)>0;
(2)从最高点到入水,离水面的高度h随时间t 的增加而减小,即h(t)单调递减,相应地,v(t)=h'(t)<0.
(1)运动员从起跳到最高点,离水面的高度h随时间t的增加而增加,即h(t)单调递增,相应地,v(t)=h'(t)>0;
(2)从最高点到入水,离水面的高度h随时间t 的增加而减小,即h(t)单调递减,相应地,v(t)=h'(t)<0.
【问题2】 观察下面几个图象,探究函数的单调性和导数的正负的关系.
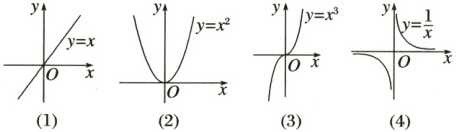
(1) $y = x$
(2) $y = x^{2}$
(3) $y = x^{3}$
(4) $y = \frac{1}{x}$
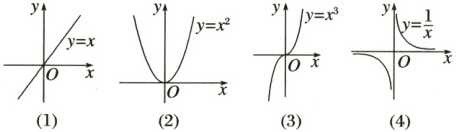
(1) $y = x$
(2) $y = x^{2}$
(3) $y = x^{3}$
(4) $y = \frac{1}{x}$
答案:
提示:
(1)函数y=x的定义域为R,并且在定义域上是增函数,其导数y'=1>0.
(2)函数y=x²的定义域为R,在(−∞,0)上单调递减,在(0,+∞)上单调递增.而y'=2x,当x<0时,其导数y'<0;当x>0时,其导数y'>0;当x=0时,其导数y'=0.
(3)函数y=x³的定义域为R,在定义域上为增函数.而y'=3x²,当x≠0时,其导数3x²>0;当x=0时,其导数3x²=0.
(4)函数y=$\frac{1}{x}$的定义域为(−∞,0)∪(0,+∞),在(−∞,0)上单调递减,在(0,+∞)上单调递减,而y'=−$\frac{1}{x²}$,因为x≠0,所以y'<0.
从以上四个函数的单调性及其导数符号的关系上说明,在区间(a,b)内,如果f'(x)>0,那么函数y=f(x)在这个区间上单调递增;如果f'(x)<0,那么函数y=f(x)在这个区间上单调递减.
(1)函数y=x的定义域为R,并且在定义域上是增函数,其导数y'=1>0.
(2)函数y=x²的定义域为R,在(−∞,0)上单调递减,在(0,+∞)上单调递增.而y'=2x,当x<0时,其导数y'<0;当x>0时,其导数y'>0;当x=0时,其导数y'=0.
(3)函数y=x³的定义域为R,在定义域上为增函数.而y'=3x²,当x≠0时,其导数3x²>0;当x=0时,其导数3x²=0.
(4)函数y=$\frac{1}{x}$的定义域为(−∞,0)∪(0,+∞),在(−∞,0)上单调递减,在(0,+∞)上单调递减,而y'=−$\frac{1}{x²}$,因为x≠0,所以y'<0.
从以上四个函数的单调性及其导数符号的关系上说明,在区间(a,b)内,如果f'(x)>0,那么函数y=f(x)在这个区间上单调递增;如果f'(x)<0,那么函数y=f(x)在这个区间上单调递减.
函数的单调性与其导数的正负之间的关系
定义在区间$(a,b)$内的函数$y = f(x)$.

定义在区间$(a,b)$内的函数$y = f(x)$.

答案:
增 减
查看更多完整答案,请扫码查看


