《2025年学易优同步学案导学高中数学选择性必修第二册通用版》

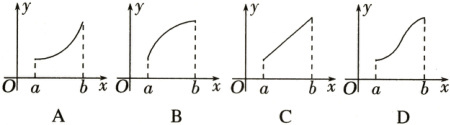
【跟踪训练2】 若函数$f(x)$的导函数在区间$[a,b]$上是增函数，则函数$f(x)$在区间$[a,b]$上的图象可能是 (A)

答案： A　函数f(x)的导函数f'(x)在
[a,b]上是增函数，
　若对任意x₁和x₂满足a＜x₁＜x₂＜b,
　则有f'(a)＜f'(x₁)＜f'(x₂)＜f'(b),
　根据导数的几何意义，可知函数y=f(x)的切线斜率在[a,b]内单调递增，
　观察图象，只有A符合.

【问题3】 如何利用$f^{\prime}(x_0)$的定义以及函数的概念给出导函数的概念?

答案： 提示:如果函数y=f(x)在开区间(a,b)
内的每点处都有导数，即任给x₀∈(a,b)，总有lim$_{\Delta x \to 0}$$\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$=f'(x₀),从而对开区间(a,b)内的每一个值x₀，都有唯一确定的函数值f'(x₀)与x₀对应,所以在开区间(a,b)内,f'(x)
构成一个新的函数——导函数f'(x).

导函数的定义
从求函数$f(x)$在$x = x_0$处导数的过程可以看出，当$x = x_0$时，$f^{\prime}(x_0)$是一个唯一确定的数. 这样，当$x$变化时，$y = f^{\prime}(x)$就是$x$的函数，我们称它为$y = f(x)$的导函数$f^{\prime}(x)$ (简称导数).$y = f(x)$的导函数记作$y'$或，即$f^{\prime}(x)=y^{\prime}=\lim_{\Delta x \to 0}\frac{f(x + \Delta x)-f(x)}{\Delta x}$.

答案： 导函数f'(x)　y'