《2025年学易优同步学案导学高中数学选择性必修第二册通用版》

2. 数列的一般形式是$a_1，a_2，·s，a_n，·s$，简记为$\{ a_{n}\}$.

答案： 2.$\{ a_{n}\}$

3. 数列的分类

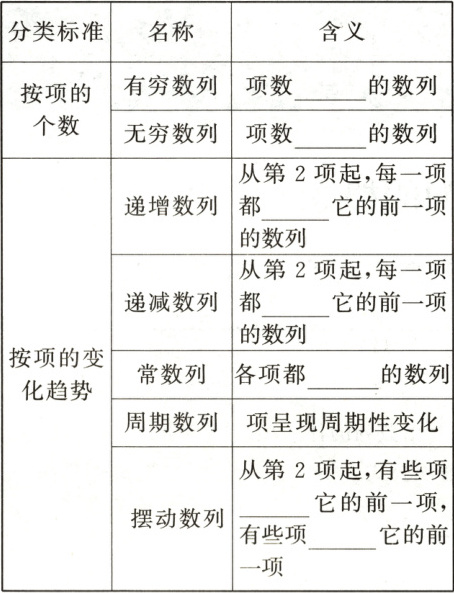
答案： 3.有限 无限 大于 小于 相等 大于 小于

【例1】 (1)(多选)以下四个数列中的递增数列是 (CD)
A.$1，\frac{1}{2}，\frac{1}{4}，\frac{1}{8}，·s$
B.$\sin \frac{π}{7}，\sin \frac{2π}{7}，\sin \frac{3π}{7}，·s$
C.$-1，-\frac{1}{2}，-\frac{1}{4}，-\frac{1}{8}，·s$
D.$1，\sqrt{2}，\sqrt{3}，·s，\sqrt{21}$
(2)给出以下数列：
①2016～2024年某市普通高中生人数(单位：万人)构成数列$82，93，105，118，132，147，163，180，198$；
②无穷多个$\sqrt{3}$构成数列$\sqrt{3}，\sqrt{3}，\sqrt{3}，\sqrt{3}，·s$；
③$-2$的1次幂，2次幂，3次幂，4次幂，$·s$构成数列$-2，4，-8，16，-32，·s$.
其中，有穷数列是①，无穷数列是②③，递增数列是①，常数列是②，摆动数列是③(填序号).

答案：
(1)CD A是递减数列;B是摆动数列;C，D是递增数列.
(2)① ②③ ① ② ③ ①为有穷数列;②③是无穷数列，同时①也是递增数列;②为常数列;③为摆动数列.

【跟踪训练1】 下列数列中哪些是有穷数列？哪些是无穷数列？哪些是递增数列？哪些是递减数列？哪些是常数列？哪些是摆动数列？
(1)$1，0.84，0.84^2，0.84^3，·s$；
(2)$2，4，6，8，10，·s$；
(3)$7，7，7，7，·s$；
(4)$\frac{1}{3}，\frac{1}{9}，\frac{1}{27}，\frac{1}{81}，·s$；
(5)$10，9，8，7，6，5，4，3，2，1$；
(6)$0，-1，2，-3，4，-5，·s$.

答案： 解：
(5)是有穷数列;
(1)
(2)
(3)
(4)
(6)是无穷数列;
(2)是递增数列;
(1)
(4)
(5)是递减数列;
(3)是常数列;
(6)是摆动数列.