《2025年同步练习册人民教育出版社高中数学选择性必修第二册人教版B专版》

1 组合的定义
一般地，从 $n$ 个不同对象中取出 $m(m\leq n)$ 个对象并成一组，称为从 $n$ 个不同对象中取出 $m$ 个对象的一个组合。
名师点津
组合的概念中有两个要点：
(1)要求 $n$ 个对象是不同的；
(2)“只取不排”，即取出的 $m$ 个对象与顺序无关。
【思考交流】怎样辨别一个问题是排列问题还是组合问题？

答案： 1.并成一组
【思考交流】
提示 辨别一个问题是排列问题还是组合问题，关键看选出的对象与顺序是否有关,若交换某一问题中某两个对象的位置对结果产生影响，则是排列问题，否则就是组合问题.

2 组合数的概念
从 $n$ 个不同对象中取出 $m$ 个对象的所有组合的个数，称为从 $n$ 个不同对象中取出 $m$ 个对象的组合数，用符号$C_n^m$表示。
【思考交流】如何理解组合与组合数这两个概念？

答案： 2.所有组合 $C_n^m$
【思考交流】
提示 同“排列”与“排列数”是两个不同的概念一样，“组合”与“组合数”也是两个不同的概念，“组合”是指“从$n$个不同对象中取$m(m\leq n)$个对象并成一组”，它不是一个数，而是具体的一件事；“组合数”是指“从$n$个不同对象中取出$m$个对象的所有组合的个数”，它是一个数.例如，从$3$个不同对象$a,b,c$中取出两个对象的组合为$ab,ac,bc$，其中每一种都叫一个组合，这些组合共有$3$个，则组合数为$3$.

3 组合数公式、性质

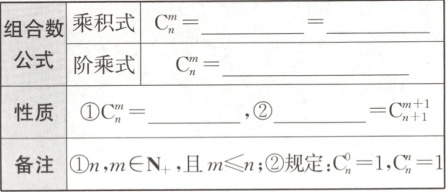
名师点津
组合数的两个性质及其应用
(1)性质①反映了组合数的对称性。若 $m＞\frac{n}{2}$，通常不直接计算 $C_{n}^{m}$，而改为计算 $C_{n}^{n - m}$，这样可以减少计算量。
(2)性质②的特点是右端下标为 $n + 1$，左端下标都为 $n$，上标相差 $1$；左端的一个上标与右端的上标一样，左端的另一个上标比它们少 $1$。
(3)要注意性质 $C_{n}^{m+1}+C_{n}^{m}=C_{n + 1}^{m+1}$ 的正用、逆用及变形用。
正用是“合二为一”；逆用是将一个组合数拆成两个。变形式 $C_{n}^{m}=C_{n + 1}^{m+1}-C_{n}^{m+1}$ 为某些项相互抵消提供了方便。在解题中要注意灵活运用。
自测反馈

答案： 3.
$A_n^m=\frac{n(n - 1)·s[n - (m - 1)]}{m×(m - 1)×·s×2×1} \quad \frac{n!}{(n - m)!m!}$
$C_n^{n - m}=C_{n + 1}^{m + 1}+C_n^m$
自测反馈

1. 判断正误。(正确的画“√”，错误的画“×”)
(1)两个组合相同的充要条件是其中的对象完全相同。(√)
(2)从 $a_{1},a_{2},a_{3}$ 三个不同元素中任取两个元素组成一个组合，所有组合的个数为 $C_{3}^{2}$。(√)
(3)“从甲、乙、丙 $3$ 名同学中选出 $2$ 名分别去参加某两个乡镇的社会调查，有多少种不同的选法？”是组合问题。(×)
(4)从甲、乙、丙 $3$ 名同学中选出 $2$ 名，有 $3$ 种不同的选法。(√)
(5)“现有 $4$ 枚相同的纪念币送给 $10$ 人中的 $4$ 人留念，有多少种送法？”是排列问题。(×)

答案： 1.
(1)√
(2)√
(3)×
(4)√
(5)×