《2025年同步练习册人民教育出版社高中数学选择性必修第二册人教版B专版》

1. 设有一正态分布，它的正态曲线是函数$f(x)$的图象，且$f(x)=\varphi_{\mu,\sigma}(x)=\frac{1}{\sqrt{8\pi}}e^{-\frac{(x - 10)^2}{8}}$，则这个正态分布的均值与标准差分别是(B).

A.$10$与$8$
B.$10$与$2$
C.$8$与$10$
D.$2$与$10$

答案： 1.B　解析由正态分布的概率密度函数的定义可知，总体的均值μ = 10，方差σ² = 4，即σ = 2.

2. 已知某批零件的长度误差(单位：$mm$)服从正态分布$N(0,3^2)$，从中随机取一件，其长度误差落在区间$[3,6]$内的概率为(B).(附：若随机变量$\xi$服从正态分布$N(\mu,\sigma^2)$，则$P(\mu-\sigma\leqslant\xi\leqslant\mu+\sigma)\approx68.3\%$，$P(\mu - 2\sigma\leqslant\xi\leqslant\mu+2\sigma)\approx95.4\%$)

A.$4.56\%$
B.$13.55\%$
C.$27.18\%$
D.$31.74\%$

答案： 2.B　解析由正态分布的概率公式，知P(−3≤ξ≤3)≈0.683，P(−6≤ξ≤6)≈0.954，故P(3≤ξ≤6)=$\frac{P(−6≤ξ≤6)−P(−3≤ξ≤3)}{2}$≈$\frac{0.954−0.683}{2}$ = 13.55%，故选B.

3. 在多次实验的结果中，某物理量的测量结果服从正态分布$N(10,\sigma^2)$，下列结论中不正确的是(D).

A.$\sigma$越小，该物理量在一次测量中在$(9.9,10.1)$的概率越大
B.$\sigma$越小，该物理量在一次测量中大于$10$的概率为$0.5$
C.$\sigma$越小，该物理量在一次测量中小于$9.99$与大于$10.01$的概率相等
D.$\sigma$越小，该物理量在一次测量中落在$(9.9,10.2)$与落在$(10,10.3)$的概率相等

答案： 3.D解析本题考查正态分布.对于A，σ²为数据的方差，所以σ越小，数据在μ = 10附近越集中，所以测量结果落在(9.9，10.1)内的概率越大，故A正确；对于B，由正态分布密度曲线的对称性可知该物理量一次测量大于10的概率为0.5，故B正确；对于C，由正态分布密度曲线的对称性可知该物理量一次测量结果大于10.01的概率与小于9.99的概率相等，故C正确；对于D，因为该物理量一次测量结果落在(9.9，10)的概率与落在(10.2，10.3)的概率不同，所以一次测量结果落在(9.9，10.2)的概率与落在(10，10.3)的概率不同，故D错误.

4. 已知在某市的高三学生学习质量检测考试中，学生的数学成绩服从正态分布$N(98,100)$，且参加本次考试的全市学生约有$9450$人，如果某学生在这次考试中的数学成绩是$108$分，那么他的数学成绩大约排在全市第(A).

A.$1500$名
B.$1700$名
C.$4500$名
D.$8000$名

答案： 4.A　解析因为学生的数学成绩X服从正态分布N(98,100)，所以P(X＞108)=$\frac{1}{2}$[1−P(88≤X≤108)]=$\frac{1}{2}$[1−P(μ−σ≤X≤μ+σ)]≈$\frac{1}{2}$×(1−0.683)=0.1585，所以0.1585×9450≈1498，观察各选项，知该学生的数学成绩大约排在全市第1500名.

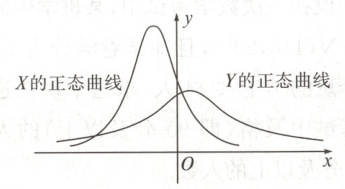
5. (多选题)设$X\sim N(\mu_1,\sigma_1^2)$，$Y\sim N(\mu_2,\sigma_2^2)$，这两个正态曲线如图所示.下列结论中不正确的是(ABD).


A.$P(Y\geqslant\mu_2)\geqslant P(Y\geqslant\mu_1)$
B.$P(X\leqslant\sigma_2)\leqslant P(X\leqslant\sigma_1)$
C.对任意正数$t$，$P(X\leqslant t)\gt P(Y\leqslant t)$
D.对任意正数$t$，$P(X\geqslant t)\gt P(Y\geqslant t)$

答案： 5.ABD　解析由题图可知μ₁＜0＜μ₂，σ₁＜σ₂，P(Y≥μ₂)＜P(Y≥μ₁)，故A错；P(X≤σ₂)＞P(X≤σ₁)，故B错；当t为任意正数时，由题图可知P(X≤t)＞P(Y≤t)，而P(X≤t)=1−P(X≥t)，P(Y≤t)=1−P(Y≥t)，故P(X≥t)＜P(Y≥t)，故C正确，D错.

6. (多选题)已知正态分布$N(\mu,\sigma^2)$的正态曲线是$f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$，$x\in R$的图象.给出以下四个命题，其中是真命题的有(ABD).

A.对任意$x\in R$，$f(\mu + x)=f(\mu - x)$成立
B.如果随机变量$X$服从$N(\mu,\sigma^2)$，且$F(x)=P(X\lt x)$，那么$F(x)$是$R$上的增函数
C.如果随机变量$X$服从$N(108,100)$，那么$X$的期望是$108$，标准差是$100$
D.随机变量$X$服从$N(\mu,\sigma^2)$，$P(X\lt1)=\frac{1}{2}$，$P(X\gt2)=p$，则$P(0\lt X\lt2)=1 - 2p$

答案： 6.ABD　解析对于X~N(μ,σ²)，则正态曲线关于直线x = μ对称，故f(μ + x)=f(μ−x).故A项正确.如果随机变量X~N(108,100)，所以μ = 108，σ² = 100，即σ = 10，故C项错.由正态分布概率密度函数性质以及概率的计算知B项，D项正确，故选ABD.