第89页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
4. 如图,已知线段 $AB = 16\ cm$,线段 $AB$ 上有一点 $C$,且 $BC = 6\ cm$,$E$ 是 $BC$ 的中点,$M$ 是 $AC$ 的中点,则 $EM$ 的长度为 \underline{

8 cm
}。
答案:
8 cm
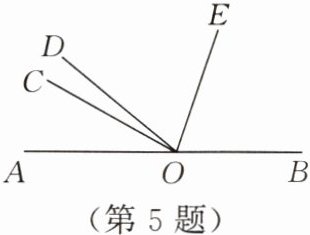
5. 如图,点 $A$,$O$,$B$ 在一条直线上,$\angle AOC = 3\angle COD$,$OE$ 平分 $\angle BOD$。若 $\angle AOC = 45^{\circ}$,求 $\angle COE$ 的度数。

答案:
解:因为∠AOC=45°,∠AOC=3∠COD,所以∠COD=$\frac{1}{3}$∠AOC=15°。因为点A,O,B在一条直线上,所以∠AOB=180°,所以∠BOD=180°-∠AOC-∠COD=180°-45°-15°=120°。因为OE平分∠BOD,所以∠DOE=$\frac{1}{2}$∠BOD=60°,所以∠COE=∠COD+∠DOE=15°+60°=75°。
6.(数学应用)阅读下表,解答后面的问题:
|线段 $AB$ 上点的个数 $n$|图例|线段总条数 $N$|
|:--:|:--:|:--:|
|3|$A$ $C$ $B$| $3 = 2 + 1$|
|4|$A$ $C$ $D$ $B$| $6 = 3 + 2 + 1$|
|5|$A$ $C$ $D$ $E$ $B$| $10 = 4 + 3 + 2 + 1$|
|6|$A$ $C$ $D$ $E$ $F$ $B$| $15 = 5 + 4 + 3 + 2 + 1$|
(1)根据表中数据猜测:线段的总条数 $N$ 与线段上的点数 $n$(包括两个端点)的关系是
(2)根据上述关系解决问题:有一辆客车往返于 $A$,$B$ 两地,中途停靠 $3$ 个站点,如果任意两站间的票价都不同。
①有
②要准备

|线段 $AB$ 上点的个数 $n$|图例|线段总条数 $N$|
|:--:|:--:|:--:|
|3|$A$ $C$ $B$| $3 = 2 + 1$|
|4|$A$ $C$ $D$ $B$| $6 = 3 + 2 + 1$|
|5|$A$ $C$ $D$ $E$ $B$| $10 = 4 + 3 + 2 + 1$|
|6|$A$ $C$ $D$ $E$ $F$ $B$| $15 = 5 + 4 + 3 + 2 + 1$|
(1)根据表中数据猜测:线段的总条数 $N$ 与线段上的点数 $n$(包括两个端点)的关系是
$N=\frac{n(n-1)}{2}$
。(2)根据上述关系解决问题:有一辆客车往返于 $A$,$B$ 两地,中途停靠 $3$ 个站点,如果任意两站间的票价都不同。
①有
10
种不同的票价;②要准备
20
种车票。
答案:
(1)N=$\frac{n(n-1)}{2}$
(2)①10 ②20 解析:①A,B两地之间有3个站点,可以看作一条线段上有5个点,则共有$\frac{5×(5-1)}{2}=10$(条)线段,即有10种票价;②考虑到往返情况,则需准备10×2=20(种)车票。
(1)N=$\frac{n(n-1)}{2}$
(2)①10 ②20 解析:①A,B两地之间有3个站点,可以看作一条线段上有5个点,则共有$\frac{5×(5-1)}{2}=10$(条)线段,即有10种票价;②考虑到往返情况,则需准备10×2=20(种)车票。
7. 如图,数轴上点 $O$ 为原点,$A$,$B$ 两点所表示的数分别为 $-2$ 和 $8$。

(1)线段 $AB$ 的长为
(2)动点 $P$ 从点 $A$ 出发,以每秒 $1$ 个单位长度的速度沿数轴向右匀速运动,设运动时间为 $t(t > 0)\ s$。
①当 $0 < t < 10$ 时,$PA =$
②若 $M$ 是线段 $PA$ 的中点,$N$ 是线段 $PB$ 的中点,试判断线段 $MN$ 的长度是否与点 $P$ 的运动时间 $t(s)$ 有关。若有关,请求出线段 $MN$ 的长度与 $t$ 的关系式;若无关,请说明理由,并求出线段 $MN$ 的长度。

(1)线段 $AB$ 的长为
10
。(2)动点 $P$ 从点 $A$ 出发,以每秒 $1$ 个单位长度的速度沿数轴向右匀速运动,设运动时间为 $t(t > 0)\ s$。
①当 $0 < t < 10$ 时,$PA =$
t
,$PB =$ 10-t
,点 $P$ 表示的数为 -2+t
。(用含 $t$ 的式子表示)②若 $M$ 是线段 $PA$ 的中点,$N$ 是线段 $PB$ 的中点,试判断线段 $MN$ 的长度是否与点 $P$ 的运动时间 $t(s)$ 有关。若有关,请求出线段 $MN$ 的长度与 $t$ 的关系式;若无关,请说明理由,并求出线段 $MN$ 的长度。
MN的长度与点P的运动时间t(s)无关。当0<t<10时,PA=t,PB=10-t,因为M,N分别是PA,PB的中点,所以PM=$\frac{t}{2}$,PN=$\frac{1}{2}(10-t)=5-\frac{t}{2}$,所以MN=PM+PN=$\frac{t}{2}+(5-\frac{t}{2})=5$。当t=10时,PA=10,即点P与点B重合,则MN=5。当t>10时,PA=t,PB=t-10,因为M,N分别是PA,PB的中点,所以PM=$\frac{t}{2}$,PN=$\frac{1}{2}(t-10)=\frac{t}{2}-5$,所以MN=PM-PN=$\frac{t}{2}-(\frac{t}{2}-5)=5$。综上所述,MN的长与点P的运动时间t(s)无关,MN的长度为5。
答案:
解:
(1)10
(2)①t 10-t -2+t ②MN的长度与点P的运动时间t(s)无关。当0<t<10时,PA=t,PB=10-t,因为M,N分别是PA,PB的中点,所以PM=$\frac{t}{2}$,PN=$\frac{1}{2}(10-t)=5-\frac{t}{2}$,所以MN=PM+PN=$\frac{t}{2}+(5-\frac{t}{2})=5$。当t=10时,PA=10,即点P与点B重合,则MN=5。当t>10时,PA=t,PB=t-10,因为M,N分别是PA,PB的中点,所以PM=$\frac{t}{2}$,PN=$\frac{1}{2}(t-10)=\frac{t}{2}-5$,所以MN=PM-PN=$\frac{t}{2}-(\frac{t}{2}-5)=5$。综上所述,MN的长与点P的运动时间t(s)无关,MN的长度为5。
(1)10
(2)①t 10-t -2+t ②MN的长度与点P的运动时间t(s)无关。当0<t<10时,PA=t,PB=10-t,因为M,N分别是PA,PB的中点,所以PM=$\frac{t}{2}$,PN=$\frac{1}{2}(10-t)=5-\frac{t}{2}$,所以MN=PM+PN=$\frac{t}{2}+(5-\frac{t}{2})=5$。当t=10时,PA=10,即点P与点B重合,则MN=5。当t>10时,PA=t,PB=t-10,因为M,N分别是PA,PB的中点,所以PM=$\frac{t}{2}$,PN=$\frac{1}{2}(t-10)=\frac{t}{2}-5$,所以MN=PM-PN=$\frac{t}{2}-(\frac{t}{2}-5)=5$。综上所述,MN的长与点P的运动时间t(s)无关,MN的长度为5。
8.(综合与实践)如图①,已知点 $O$ 为直线 $AB$ 上一点,$OC$ 在直线 $AB$ 的上方,$\angle AOC = 60^{\circ}$。一直角三角尺的直角顶点放在点 $O$ 处,三角尺的一边 $OM$ 在射线 $OB$ 上,另一边 $ON$ 在直线 $AB$ 的下方。

(1)在图①中,$\angle BOC$ 的度数为
(2)如图②,当三角尺绕点 $O$ 旋转至一边 $OM$ 恰好平分 $\angle BOC$ 时,$\angle BON$ 的度数为
(3)如图③,当三角尺绕点 $O$ 旋转至一边 $ON$ 在 $\angle AOC$ 的内部时,$\angle AOM - \angle CON$ 的度数为

(1)在图①中,$\angle BOC$ 的度数为
120°
,$\angle CON$ 的度数为150°
;(2)如图②,当三角尺绕点 $O$ 旋转至一边 $OM$ 恰好平分 $\angle BOC$ 时,$\angle BON$ 的度数为
30°
;(3)如图③,当三角尺绕点 $O$ 旋转至一边 $ON$ 在 $\angle AOC$ 的内部时,$\angle AOM - \angle CON$ 的度数为
30°
。
答案:
(1)120° 150°
(2)30°
(3)30°
(1)120° 150°
(2)30°
(3)30°
查看更多完整答案,请扫码查看


