《2025年课堂精练七年级数学上册北师大版四川专版》

1. 有理数的乘方
求$n$个相同因数$a$的积的运算叫作乘方。
形式：$a^{n}$，其中$a$为底数，$n$为指数。

答案： 乘方 底数 指数

2. 乘方的运算法则
正数的任何次幂都是正数。
负数的奇次幂为负数，偶次幂为正数。$0$的正整数次幂为0。

答案： 正数 负数 正数 0

1. $(-2)^{4}$表示的意义是（A）。
A.$(-2)×(-2)×(-2)×(-2)$
B.$(-2)+(-2)+(-2)+(-2)$
C.$(-2)×4$
D.$2×2×2×2$

答案： A

2. 下列各组数中，互为相反数的一组是（C）。
A.$3^{2}$与$-2^{3}$
B.$-(-2)$与$\vert -2\vert$
C.$(-2)^{2}$与$-2^{2}$
D.$-\dfrac{1^{2}}{3}$与$\left(\dfrac{1}{3}\right)^{2}$

答案： C

3. 下列运算正确的是（D）。
A.$(-3)^{2}=-9$
B.$-(-2)^{2}=4$
C.$3^{2}=6$
D.$2^{3}=8$

答案： D

4. （1）$2^{6}$中，底数是2，指数是6，读作2的6次幂；
（2）$(-2)^{5}$中，底数是-2，指数是5，读作-2的5次幂；
（3）$-2^{4}$中，底数是2，指数是4，读作2的4次幂的相反数。

答案：
(1)2 6 2的6次幂
(2)-2 5 -2的5次幂
(3)2 4 2的4次幂的相反数

5. 若$\vert b - 2\vert$与$(a + 3)^{2}$互为相反数，则$-a^{b}$的值为-9。

答案： -9

6. 将$-\dfrac{1}{2}$，$\vert -2.5\vert$，$0$，$-2^{2}$，$-(-4)$，$3$用“$＜$”连接起来：$-2^{2}＜-\frac {1}{2}＜0＜|-2.5|＜3＜-(-4)$。

答案： $-2^{2}＜-\frac {1}{2}＜0＜|-2.5|＜3＜-(-4)$

7. 计算：
（1）$(-2)^{2}×(-5)$；
（2）$(-3)^{3}-3×\left(-\dfrac{1}{3}\right)^{4}$；
（3）$-1^{4}-\dfrac{1}{6}×[2-(-3)]^{2}$。

答案： 解:
(1)原式$=4×(-5)=-20$。
(2)原式$=-27-\frac {1}{27}=-27\frac {1}{27}$。
(3)原式$=-1-\frac {1}{6}×(2+3)^{2}=-1-\frac {1}{6}×5^{2}=-1-\frac {1}{6}×25=-1-\frac {25}{6}=-\frac {31}{6}$。

8. （数学应用）小明爸爸给小明列了一张表，说明他本月炒股的盈亏情况（单位：元）。

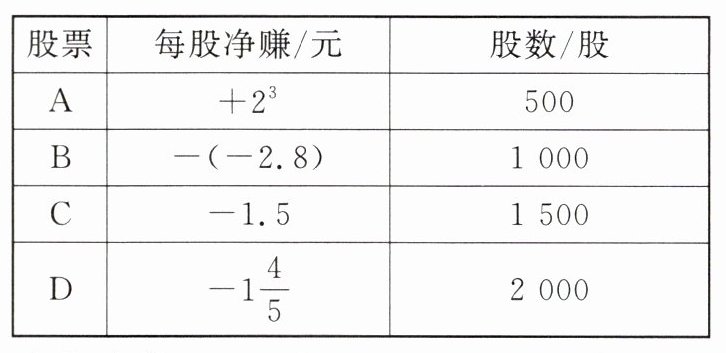
请你计算一下，小明爸爸本月投资炒股到底是赔了还是赚了？赔了或赚了多少元？

答案： 解:$2^{3}×500+2.8×1000-1.5×1500-1\frac {4}{5}×2000$
$=4000+2800-2250-3600$
$=950$(元)。
故小明爸爸本月投资炒股赚了,赚了950元。