《2025年课堂精练七年级数学上册北师大版四川专版》

有理数减法法则：
减一个数，等于加这个数的相反数。

答案： 相反数

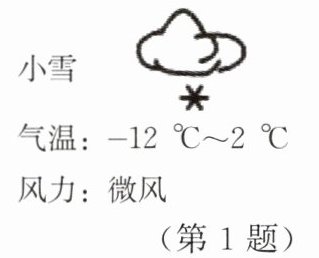
1. 我市 12 月某天的天气预报如图所示，则该天最高气温比最低气温高（B）。

A.$-9\ \degree C$
B.$14\ \degree C$
C.$9\ \degree C$
D.$-14\ \degree C$

答案： B

2. 下列各式的计算结果为负数的是（D）。
A.$-3-(-7)$
B.$|-2-(-1)|$
C.$-(-3-2)$
D.$-2+(-4)$

答案： D

3. 下列说法正确的是（B）。
A.两个有理数的差一定小于被减数
B.若两数差为 0，则这两个数必相等
C.互为相反数的两数相减，差必为 0
D.若两数的差为正，则被减数必为正

答案： B

4. 在下列括号内填上适当的数。
(1) $(-7)-(-3)=$（-7）$+3$；
(2) $(-5)-4=(-5)+$（-4）；
(3) $0-(-2.5)=0+$（2.5）；
(4) $8-(+213)=8+$（-213）。

答案：
(1)-7；
(2)-4；
(3)2.5；
(4)-213

5. 计算：
(1) $35-47=$-12；
(2) $(-5)-(-9)=$4；
(3) $0-(-52)=$52。

答案：
(1)-12；
(2)4；
(3)52

6. 符号“$f$”表示一种运算，它对一些数的运算结果如下：
(1) $f(1)=0$，$f(2)=1$，$f(3)=2$，$f(4)=3$，$\cdots$；
(2) $f\left(\dfrac{1}{2}\right)=2$，$f\left(\dfrac{1}{3}\right)=3$，$f\left(\dfrac{1}{4}\right)=4$，$f\left(\dfrac{1}{5}\right)=5$，$\cdots$。
利用以上规律计算：
$f\left(\dfrac{1}{223}\right)-f(224)=$0。

答案： 0

7. (数学应用)某超市出售三种品牌的大米，袋上分别标有质量为$(25\pm0.1)kg$，$(25\pm0.2)kg$，$(25\pm0.3)kg$的字样，其中任意拿出两袋，它们的质量最多相差0.6 kg。

答案： 0.6 kg

8. 计算：
(1) $\left(+\dfrac{4}{7}\right)-3\ \dfrac{1}{3}$；
(2) $-(-2.41)-\vert -3.72\vert$；
(3) $(-3)-\left(-\dfrac{1}{3}\right)+(-1)-\dfrac{1}{3}$。

答案： 1. （1）
解：
首先将带分数化为假分数：$3\frac{1}{3}=\frac{10}{3}$。
然后根据有理数减法法则$a - b=a+( - b)$，$(+\frac{4}{7})-3\frac{1}{3}=\frac{4}{7}+(-\frac{10}{3})$。
通分：$\frac{4}{7}+(-\frac{10}{3})=\frac{4×3}{7×3}+(-\frac{10×7}{3×7})=\frac{12}{21}+(-\frac{70}{21})$。
计算：$\frac{12 - 70}{21}=-\frac{58}{21}=-2\frac{16}{21}$。
2. （2）
解：
根据去括号法则$-(-a)=a$，$-(-2.41)=2.41$；根据绝对值的性质$\vert - a\vert=a(a\geq0)$，$\vert - 3.72\vert = 3.72$。
则$-(-2.41)-\vert - 3.72\vert=2.41 - 3.72$。
计算：$2.41-3.72=-(3.72 - 2.41)=-1.31$。
3. （3）
解：
根据有理数减法法则$a - b=a+( - b)$，$(-3)-(-\frac{1}{3})+(-1)-\frac{1}{3}=(-3)+\frac{1}{3}+(-1)+(-\frac{1}{3})$。
利用加法结合律$(a + b)+c=a+(b + c)$，$[(-3)+(-1)]+[\frac{1}{3}+(-\frac{1}{3})]$。
计算：$(-4)+0=-4$。
综上，（1）的结果是$-2\frac{16}{21}$；（2）的结果是$-1.31$；（3）的结果是$-4$。

9. 对于含绝对值的算式，在有些情况下，可以不需要计算出结果也能将绝对值符号去掉，例如：$|7-6|=7-6$；$|6-7|=7-6$；$\left|\dfrac{1}{2}-\dfrac{1}{3}\right|=\dfrac{1}{2}-\dfrac{1}{3}$；$\left|\dfrac{1}{3}-\dfrac{1}{2}\right|=\dfrac{1}{2}-\dfrac{1}{3}$。
观察上述式子的特征，解答下列问题：
(1) 把下列各式写成去掉绝对值符号的形式(不用写出计算结果)：
① $|23-47|=$47-23；
② $\left|\dfrac{2}{3}-\dfrac{2}{5}\right|=$$\frac{2}{3}-\frac{2}{5}$。
(2) 当$a＞b$时，$|a-b|=$$a-b$；
当$a＜b$时，$|a-b|=$$b-a$。
(3) 计算：
$\left|\dfrac{1}{2}-1\right|+\left|\dfrac{1}{3}-\dfrac{1}{2}\right|+\left|\dfrac{1}{4}-\dfrac{1}{3}\right|+\cdots+\left|\dfrac{1}{204}-\dfrac{1}{203}\right|$。
原式$=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\cdots +\frac{1}{203}-\frac{1}{204}=1-\frac{1}{204}=\frac{203}{204}$

答案：
(1)①47-23 ②$\frac{2}{3}-\frac{2}{5}$；
(2)$a-b$ $b-a$；
(3)原式$=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\cdots +\frac{1}{203}-\frac{1}{204}=1-\frac{1}{204}=\frac{203}{204}$