第15页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1. 图形绕着给定的直线旋转一周后形成的几何体是(
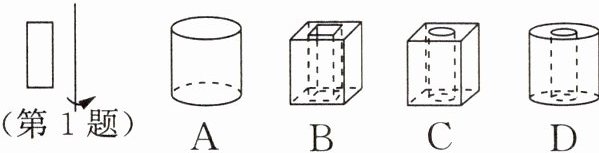
D
)。
答案:
D
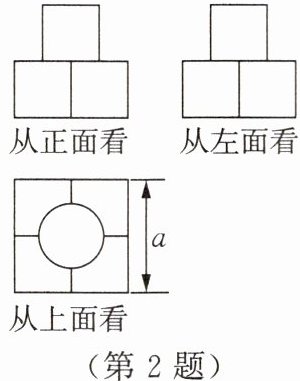
2. (数学应用)从正面、左面和上面看一个几何体的形状图如图所示。
(1)请描述这个几何体的形状;
(2)请根据图中标注的数据,计算这个几何体的表面积。
(1)请描述这个几何体的形状;
(2)请根据图中标注的数据,计算这个几何体的表面积。

答案:
解:
(1)这个几何体是由四个小正方体上面摆放了一个圆柱构成的。
(2)$4a^{2}+\frac {1}{4}\pi a^{2}$。
(1)这个几何体是由四个小正方体上面摆放了一个圆柱构成的。
(2)$4a^{2}+\frac {1}{4}\pi a^{2}$。
3. 已知直四棱柱底面边长都为2 cm,侧棱长为5 cm,则它的侧面展开图的面积为
$40cm^{2}$
。
答案:
$40cm^{2}$
4. (数学游戏)在学习了立体图形及其展开图后,喜爱数学的小明和同桌制作了如图①所示的正方体,并在正方体的内表面写上“祝你学习进步”六个字,玩起了猜字的游戏。他们将表面适当剪开,得到如图②所示的表面展开图。请回答下列问题:
(1)“你”的对面是“
(2)如果“祝”是左面,“你”在后面,那么“
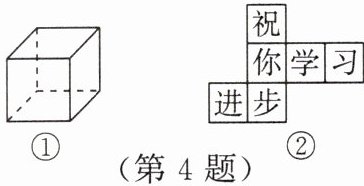
(1)“你”的对面是“
习
”,“你”的相邻面是“祝、学、进、步
”;(2)如果“祝”是左面,“你”在后面,那么“
学
”在上面。
答案:
(1)习 祝、学、进、步
(2)学
(1)习 祝、学、进、步
(2)学
5. (综合与实践)喜爱数学的小明一天在家里发现他妈妈刚从超市买回来的2块一样的肥皂,小明仔细看了肥皂盒上的尺寸说明,每块尺寸:长、宽、高分别是16 cm,6 cm,3 cm。他想起老师讲过关于物体外包装用料最省的问题,就想研究如何摆放这2个肥皂盒才能使它们的包装用料最省。
小明动手摆放了这2个肥皂盒,发现无论怎样放置,体积都不会发生变化,但是不同的摆放位置,它们的包装用料不一样。经过实际操作,小明发现这2个肥皂盒有3种不同的摆放方式,如图所示。
(1)请你帮助小明指出图①、图②、图③这3种不同摆放方式的长、宽、高,并计算包装它们的用料的表面积,填写在下表中(包装接头用料忽略不计):
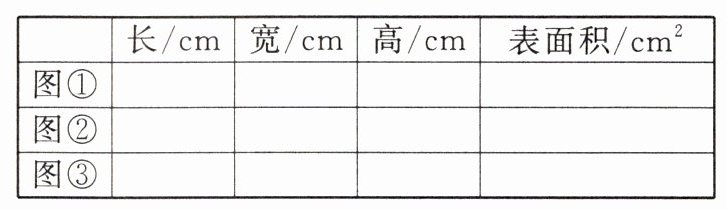
(2)探究与思考:若现在有4个这样的肥皂盒,如何摆放才能使它们的包装用料最省?说说你的理由。
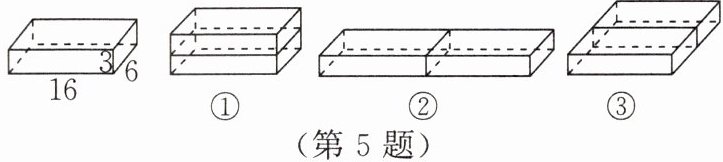
小明动手摆放了这2个肥皂盒,发现无论怎样放置,体积都不会发生变化,但是不同的摆放位置,它们的包装用料不一样。经过实际操作,小明发现这2个肥皂盒有3种不同的摆放方式,如图所示。
(1)请你帮助小明指出图①、图②、图③这3种不同摆放方式的长、宽、高,并计算包装它们的用料的表面积,填写在下表中(包装接头用料忽略不计):

(2)探究与思考:若现在有4个这样的肥皂盒,如何摆放才能使它们的包装用料最省?说说你的理由。

答案:
解:
(1)①16 6 6 456 ②32 6 3 612 ③16 12 3 552
(2)如图,将最大的面重叠在一起摆放,能使它们的包装用料最省。

解:
(1)①16 6 6 456 ②32 6 3 612 ③16 12 3 552
(2)如图,将最大的面重叠在一起摆放,能使它们的包装用料最省。

查看更多完整答案,请扫码查看


