《2025年课堂精练七年级数学上册北师大版四川专版》

9. (数学文化)古希腊数学家把数$1$，$3$，$6$，$10$，$15$，$21$，$\cdots$叫作三角形数，它有一定的规律。若把第一个三角形数记为$a_{1}$，第二个三角形数记为$a_{2}\cdots\cdots$第$n$个三角形数记为$a_{n}$，计算$a_{1}+a_{2}$，$a_{2}+a_{3}$，$a_{3}+a_{4}$，由此推算$a_{399}+a_{400}=$160000。

答案： 160000

10. $a$是不为$2$的有理数，我们把$\frac{2}{2 - a}$称为$a$的“哈利数”。如：$3$的“哈利数”是$\frac{2}{2 - 3}=-2$，$-2$的“哈利数”是$\frac{2}{2-(-2)}=\frac{1}{2}$。已知$a_{1}=3$，$a_{2}$是$a_{1}$的“哈利数”，$a_{3}$是$a_{2}$的“哈利数”，$a_{4}$是$a_{3}$的“哈利数”，依此类推，则$a_{240}=$4/3。

答案： 4/3

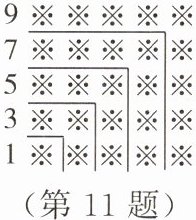
11. 观察下面由“※”组成的图案和算式，解答问题：
$1 + 3 = 4 = 2^{2}$；
$1 + 3 + 5 = 9 = 3^{2}$；
$1 + 3 + 5 + 7 = 16 = 4^{2}$；
$1 + 3 + 5 + 7 + 9 = 25 = 5^{2}$。

(1)请猜想$1 + 3 + 5 + 7 + 9 + \cdots + 19=$100；
(2)请猜想$1 + 3 + 5 + 7 + 9 + \cdots + (2n - 1)+(2n + 1)=$$(n+1)^2$；
(3)请用上述规律计算：$51 + 53 + 55 + \cdots + 97 + 99$。
原式=1+3+5+…+97+99-(1+3+5+…+49)=((99+1)/2)² - ((49+1)/2)²=50² - 25²=1875。

答案：
(1)100；
(2)(n+1)²；
(3)原式=1+3+5+…+97+99-(1+3+5+…+49)=((99+1)/2)² - ((49+1)/2)²=50² - 25²=1875。

12. (综合与实践)【阅读】求值：$1 + 2 + 2^{2}+2^{3}+2^{4}+\cdots+2^{10}$。
解：设$S = 1 + 2 + 2^{2}+2^{3}+2^{4}+\cdots+2^{10}$①，
将等式①的两边同时乘$2$，得$2S = 2 + 2^{2}+2^{3}+2^{4}+\cdots+2^{11}$②，
由②$-$①，得$2S - S = 2^{11}-1$。
即$S = 1 + 2 + 2^{2}+2^{3}+2^{4}+\cdots+2^{10}=2^{11}-1$。
(1)【运用】仿照此法计算：$1 + 3 + 3^{2}+3^{3}+3^{4}+\cdots+3^{100}$。
(2)【延伸】如图，将边长为$1$的正方形分成$4$个完全一样的小正方形，得到左上角一个小正方形为$S_{1}$，选取右下角的小正方形进行第二次操作，又得到左上角更小的正方形$S_{2}$，依次操作$2420$次，得到小正方形$S_{1}$，$S_{2}$，$S_{3}$，$\cdots$，$S_{2420}$，完成下列问题：
a. 小正方形$S_{2420}$的面积等于$\frac{1}{4^{2420}}$；
b. 求正方形$S_{1}$，$S_{2}$，$S_{3}$，$\cdots$，$S_{2420}$的面积和。
]

答案：
(1)解:设S=1+3+3²+3³+3⁴+…+3¹⁰⁰①,①×3,得3S=3+3²+3³+3⁴+…+3¹⁰¹②,由②-①得2S=3¹⁰¹-1,则S=(3¹⁰¹-1)/2。
(2)a.1/4²⁴²⁰ 解析:由图形可知,S₁=1/4,S₂=1/4×1/4=1/4²,S₃=1/4²×1/4=1/4³,…所以S₂₄₂₀=1/4²⁴²⁰,故答案为1/4²⁴²⁰。b.解:设S=1/4 + 1/4² + 1/4³ +…+1/4²⁴²⁰③,③×1/4得1/4S=1/4² + 1/4³ +…+1/4²⁴²¹④,由③-④得3/4S=1/4 - 1/4²⁴²¹,所以S=4/3(1/4 - 1/4²⁴²¹)=1/3(1 - 1/4²⁴²⁰),即S=1/3(1 - 1/4²⁴²⁰)。