《2025年课堂精练七年级数学上册北师大版四川专版》

7. 如图,将一串有理数按下列规律排列,回答下列问题:

(1) 在 $ A $ 处的数是正数还是负数?
(2) 负数排在 $ A,B,C,D $ 中的什么位置?
(3) 第 2 025 个数是正数还是负数? 排在对应于 $ A,B,C,D $ 中的什么位置?

答案：
(1)正数;
(2)B和D处;
(3)负数,B处。

8. 如图,由图①到图②是一个正方形衍生出两个小正方形,图③是图②中每个新生小正方形再衍生出两个正方形,依此规律,图⑦中共有正方形 127个。

答案： 127

9. 一组数按如图所示的方式排列,请回答下列问题。

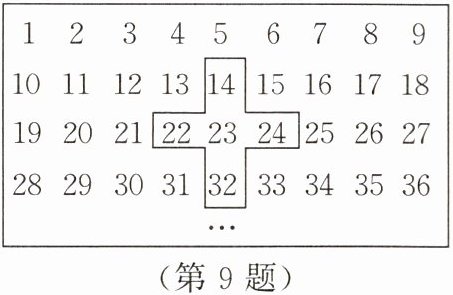
(1) 从上往下,从左到右数 2 024 在第 225行,第 8列。
(2) 由 5 个数组成的“十”字图形中。
① 这 5 个数的和可能是 2 025 吗? 为什么?
② 如果这 5 个数的和是 60,请直接写出这 5 个数。
(3) 这 5 个数的和能否是 2 035? 若能,请求出这 5 个数;若不能,请说明理由。
(2)①设中间的那个数为n,则5个数之和为5n,2025可以被5整除,但因为求出的中间数405是9的倍数,正好是第45行最后一个,无法找到构成"十字图形的5个数,所以这5个数的和不可能是2025。②这5个数的和是60,中间数为12,这5个数分别为3,11,12,13,21。(3)设中间那个数为a,则5个数之和为5a,2035能被5整除,且求出的数不在第一行,也不在其他行的行首和行尾,故这5个数为398,406,407,408,416。

答案： 解:
(1)225 8
(2)①设中间的那个数为n,则5个数之和为5n,
2025可以被5整除,但因为求出的中间数405是9的倍数,正好是第45行最后一个,无法找到构成"十字图形的5个数,所以这5个数的和不可能是2025。
②这5个数的和是60,中间数为12,这5个数分别为3,11,12,13,21。
(3)设中间那个数为a,则5个数之和为5a,
2035能被5整除,且求出的数不在第一行,也不在其他行的行首和行尾,故这5个数为398,406,407,408,416。

10. (综合与实践)图①是一个三角形,分别连接这个三角形三边的中点得到图②,再分别连接图②中间小三角形三边的中点,得到图③。

(1) 图②有 5个三角形;图③有 9个三角形。
(2) 按上面的方法继续下去,第 $ n $ 个图形中有多少个三角形? (用含 $ n $ 的代数式表示)
(3) 按此规律是否存在一个图形有 2 026 个三角形? 如果存在,请求出是第几个图形;如果不存在,请说明理由。

答案： 解:
(1)5 9
(2)第2个图形有$1+4=5$(个)三角形,第3个图形有$1+4+4=1+4×2=9$(个)三角形,所以第n个图形有$4×(n-1)+1=(4n-3)$(个)三角形。
(3)令$4n-3=2026$,解得$n=507... ... 1,$
因为不能整除,所以不存在一个图形有2026个三角形。