《2025年课堂精练七年级数学上册北师大版四川专版》

1. 去括号法则
（1）括号前是“+”，把括号和它前面的“+”去掉后，原括号里各项的符号都不改变；
（2）括号前是“-”，把括号和它前面的“-”去掉后，原括号里各项的符号都要改变。

答案：
(1)“+” 不改变
(2)括号 “-” 要改变

2. 添括号法则
（1）所添括号前面是“+”，括到括号里的各项的符号都不改变；
（2）所添括号前面是“-”，括到括号里的各项的符号都要改变。

答案：
(1)不改变
(2)要改变

1. 下列去括号正确的是（B）。
A.$a+(-2b+c)=a+2b+c$
B.$a-(-2b+c)=a+2b-c$
C.$a-2(-2b+c)=a+4b+2c$
D.$a-2(-2b+c)=a+4b-c$

答案： B

2. 与代数式 $1 - m + m^2$ 相等的式子是（B）。
A.$1-(-m+m^2)$
B.$1-(m - m^2)$
C.$1-(m + m^2)$
D.$1-(-m - m^2)$

答案： B

3. 若长方形的周长为 $6m$，一边长为 $m + n$，则与之相邻的一边长为（D）。
A.$3m + n$
B.$2m + 2n$
C.$m + 3n$
D.$2m - n$

答案： D

4. （1）$1 - 2a + a^2=-($-1+2a-a²$)=1+($_________-2a+a²$)$；
（2）$-x^2 - 2x + 3=-($x²+2x$)+3$。

答案：
(1)-1+2a-a² -2a+a²
(2)x²+2x

5. 如图，白色长方形纸片上放了两个完全相同的灰色长方形纸片，那么剩余白色长方形的周长为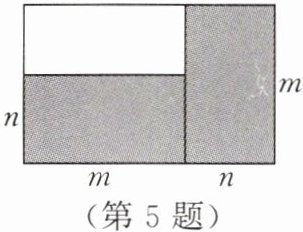4m-2n。

答案： 4m-2n

6. $m$，$n$ 互为相反数，则 $-(3m - 2n)+(2m - 3n)=$0。

答案： 0

7. 去括号，合并同类项。
（1）$-3(2s - 5)+6s$；
（2）$3x-\left[5x-\left(\frac{1}{2}x - 4\right)\right]$；
（3）$6a^2 - 4ab - 4\left(2a^2+\frac{1}{2}ab\right)$。

答案： 解:
(1)-3(2s-5)+6s=-6s+15+6s=15。$(2)3x-[5x-(\frac{1}{2}x - 4)]=3x-(5x-\frac{1}{2}x+4)=3x-5x+\frac{1}{2}x-4=-\frac{3}{2}x-4。$$(3)6a²-4ab-4(2a²+\frac{1}{2}ab)=6a²-4ab-8a²-2ab=-2a²-6ab。$

8. 已知一个三角形的第一条边长为 $3a + b$，第二条边比第一条边短 $a - 2b$，第三条边比第二条边长 $2a + b$。
（1）则第二条边长为$2a+3b$，第三条边的边长为$4a+4b$；
（2）用含 $a$，$b$ 的式子表示这个三角形的周长，并化简；
（3）若 $a$，$b$ 满足 $|a - 8|+(b - 7)^2 = 0$，求这个三角形的周长。
（2）该三角形的周长为$(3a+b)+(2a+3b)+(4a+4b)=3a+b+2a+3b+4a+4b=9a+8b$。
（3）由题意可知$a=8,b=7$，故该三角形的周长为$9×8+8×7=128$。

答案： 解:
(1)第二条边长为(3a+b)-(a-2b)=3a+b-a+2b=2a+3b，第三条边长为(2a+3b)+(2a+b)=2a+3b+2a+b=4a+4b。
(2)该三角形的周长为(3a+b)+(2a+3b)+(4a+4b)=3a+b+2a+3b+4a+4b=9a+8b。
(3)由题意可知a=8,b=7，故该三角形的周长为9×8+8×7=128。