《2025年课堂精练七年级数学上册北师大版四川专版》

9. 阅读理解：规定两数$a$，$b$之间的一种运算，记作$(a,b)$；如果$a^{c}=b$，那么$(a,b)=c$。例如：因为$2^{3}=8$，所以$(2,8)=3$。根据上述规定，若$(x,64)=3$，则$x=$4。

答案： 4

10. （数学应用）你喜欢吃拉面吗？拉面馆的师傅用一根很粗的面把两头捏合在一起拉伸，再捏合，再拉伸，反复几次，就把这根很粗的面拉成了很多根细的面条，如图所示。

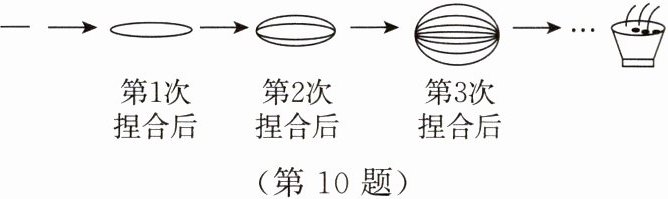
这样捏合到第7次后可拉出$128$根细面条。

答案： 7

11. 观察下列两组算式：
①$2^{2}×3^{2}$与$(2×3)^{2}$；
②$\left(-\dfrac{1}{2}\right)^{2}×2^{2}$与$\left[\left(-\dfrac{1}{2}\right)×2\right]^{2}$。
（1）每组两个算式的结果是否相等？
（2）根据（1）的结果猜想$a^{n}b^{n}$等于什么？
（3）用（2）的结论计算$\left(\dfrac{1}{5}\right)^{914}×(-5)^{914}$。

答案： 解:
(1)$2^{2}×3^{2}=4×9=36,(2×3)^{2}=6^{2}=36;$
$\left(-\dfrac{1}{2}\right)^{2}×2^{2}=\dfrac{1}{4}×4=1,\left[\left(-\dfrac{1}{2}\right)×2\right]^{2}=(-1)^{2}=1$。
所以每组两个算式的结果是相等的。
(2)根据
(1)的结果可得:$a^{n}b^{n}=(ab)^{n}$。
(3)$\left(\dfrac{1}{5}\right)^{914}×(-5)^{914}=\left[\dfrac{1}{5}×(-5)\right]^{914}=(-1)^{914}=1$。

12. （综合与实践）你能比较$1014^{1013}$和$1013^{1014}$两个数的大小吗？为了解决这个问题，我们首先把它抽象成一般形式，即比较$(n + 1)^{n}$和$n^{n + 1}$的大小（$n$为正整数），我们从分析简单的情形入手，即通过对$n = 1$，$n = 2$，$n = 3$，$\cdots$的分析，从中发现规律，经过归纳，猜想出结论。
（1）计算，比较下列各组数中两个数大小（在空格中填“$＞$”“$＜$”或“$=$”）：$1^{2}$＜$2^{1}$，$2^{3}$＜$3^{2}$，$3^{4}$＞$4^{3}$，$4^{5}$＞$5^{4}$，$5^{6}$＞$6^{5}$，$\cdots$。
（2）从（1）中结果进行归纳猜想，$n^{n + 1}$和$(n + 1)^{n}$的大小关系是$n^{n+1}＜(n+1)^{n}(n＜3);n^{n+1}＞(n+1)^{n}(n＞3$或$n=3)$。
（3）根据（1）中归纳猜想的一般结论，比较$1014^{1013}$和$1013^{1014}$的大小。
根据上面归纳猜想的一般结论可知$1014^{1013}＜1013^{1014}$。

答案： 解:
(1)＜ ＜ ＞ ＞ ＞
(2)$n^{n+1}＜(n+1)^{n}(n＜3);n^{n+1}＞(n+1)^{n}(n＞3$或$n=3)$
(3)根据上面归纳猜想的一般结论可知$1014^{1013}＜1013^{1014}$。

13. （综合与实践）如图，将一个边长为$1$的正方形纸片分割成$7$个部分，部分①是边长为$1$的正方形纸片面积的一半，部分②是部分①面积的一半，部分③是部分②面积的一半，依此类推。
（1）图中阴影部分面积为$\dfrac{1}{8}$。
（2）受此启发，你能求出$\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\cdots+\dfrac{1}{2^{6}}$的值吗？
解：由图形可得$\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\cdots+\dfrac{1}{2^{6}}=1-\dfrac{1}{2^{6}}=1-\dfrac{1}{64}=\dfrac{63}{64}$。
（3）$\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\cdots+\dfrac{1}{2^{n}}$的值为多少？（用含$n$的式子表示）
解：$\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\cdots+\dfrac{1}{2^{n}}=1-\dfrac{1}{2^{n}}$。

答案：
(1)$\dfrac{1}{8}$解析:因为部分①的面积为$\dfrac{1}{2}$,部分②的面积为$\dfrac{1}{2^{2}}=\dfrac{1}{4}$,所以部分③的面积为$\dfrac{1}{2^{3}}=\dfrac{1}{8}$,故答案为$\dfrac{1}{8}$。
(2)解:由图形可得$\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\cdots+\dfrac{1}{2^{6}}=1-\dfrac{1}{2^{6}}=1-\dfrac{1}{64}=\dfrac{63}{64}$。
(3)解:$\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\cdots+\dfrac{1}{2^{n}}=1-\dfrac{1}{2^{n}}$。