第68页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1. 观察下列一组数:$1$,$-2$,$3$,$-4$,$5$,$-6$,$7$,$-8$,$\cdots$,则第$100$个数是(
A.$100$
B.$-100$
C.$101$
D.$-101$
B
)。A.$100$
B.$-100$
C.$101$
D.$-101$
答案:
B
2. 已知下列一组数:$1$,$\frac{3}{4}$,$\frac{5}{9}$,$\frac{7}{16}$,$\frac{9}{25}$,$\cdots$,则第$n$个数为(
A.$\frac{2n - 1}{n}$
B.$\frac{n^{2}-4}{n^{2}}$
C.$\frac{2n - 1}{n^{2}}$
D.$\frac{2n + 1}{n^{2}}$
C
)。A.$\frac{2n - 1}{n}$
B.$\frac{n^{2}-4}{n^{2}}$
C.$\frac{2n - 1}{n^{2}}$
D.$\frac{2n + 1}{n^{2}}$
答案:
C
3. 观察图中的“品”字形中数之间的规律,根据观察到的规律得出$a$的值为(
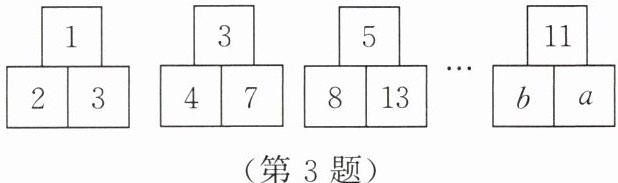
A.$75$
B.$89$
C.$103$
D.$139$
A
)。
A.$75$
B.$89$
C.$103$
D.$139$
答案:
A
4. 观察一列单项式:$-x$,$3x^{2}$,$-5x^{3}$,$7x$,$-9x^{2}$,$11x^{3}$,$\cdots$,则第$260$个单项式是
519x²
。
答案:
519x²
5. 仔细观察下列等式。
第一个:$2^{2}-1 = 1×3$;
第二个:$3^{2}-1 = 2×4$;
第三个:$4^{2}-1 = 3×5$;
第四个:$5^{2}-1 = 4×6$;
第五个:$6^{2}-1 = 5×7$;
$\cdots\cdots$
这些等式反映出自然数间的某种运算规律。设$n(n\gt1)$为自然数,则第$n$个等式可表示为
第一个:$2^{2}-1 = 1×3$;
第二个:$3^{2}-1 = 2×4$;
第三个:$4^{2}-1 = 3×5$;
第四个:$5^{2}-1 = 4×6$;
第五个:$6^{2}-1 = 5×7$;
$\cdots\cdots$
这些等式反映出自然数间的某种运算规律。设$n(n\gt1)$为自然数,则第$n$个等式可表示为
(n+1)²-1=n(n+2)
。
答案:
(n+1)²-1=n(n+2)
6. (跨学科)瑞士数学教师巴尔末成功地从光谱数据$\frac{9}{5}$,$\frac{16}{12}$,$\frac{25}{21}$,$\frac{36}{32}$,$\cdots$中,发现规律得到巴尔末公式,从而打开了光谱奥妙的大门,请按这种规律写出第$5$个数据是
49/45
。
答案:
49/45
7. (数学游戏)自然数中,有很多奇妙有趣的现象,很多秘密等待着我们去探索。比如对任意一个自然数,先将其各位数字求和,再将其和乘$3$加$2$,多次重复这种运算,最终会得到一个固定不变的数,是不是很神奇?请你试着算一算这个固定不变的数是什么。
答案:
26
8. 已知:$\frac{1}{1×2}=1-\frac{1}{2}$,$\frac{1}{2×3}=\frac{1}{2}-\frac{1}{3}$,$\frac{1}{3×4}=\frac{1}{3}-\frac{1}{4}$。
(1)$\frac{1}{n(n + 1)}=$
(2)当$n = 300$时,$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+\cdots+\frac{1}{n(n + 1)}$的值是多少?
(1)$\frac{1}{n(n + 1)}=$
$\frac{1}{n}-\frac{1}{n+1}$
;(2)当$n = 300$时,$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+\cdots+\frac{1}{n(n + 1)}$的值是多少?
当$n=300$时,原式$=1 - \frac{1}{n+1}=\frac{300}{301}$。
答案:
(1)1/n - 1/(n+1);
(2)当n=300时,原式=1 - 1/(n+1)=300/301。
(1)1/n - 1/(n+1);
(2)当n=300时,原式=1 - 1/(n+1)=300/301。
查看更多完整答案,请扫码查看


