《2025年课堂精练七年级数学上册北师大版四川专版》

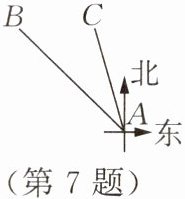
7. (数学应用)一群野生亚洲象从云南西双版纳傣族自治州走出丛林，历经 17 个月迁徙逾 500 km 安全返回栖息地。象群迁徙途经峨山县时，一头亚洲象曾脱离象群。如图，A，B，C 分别表示峨山县、象群位置、独象位置。经测量，象群在峨山县的西北方向，独象在峨山县的北偏西$15^{\circ}48'$方向，则$∠BAC=$______29°12′。

答案： 29°12′

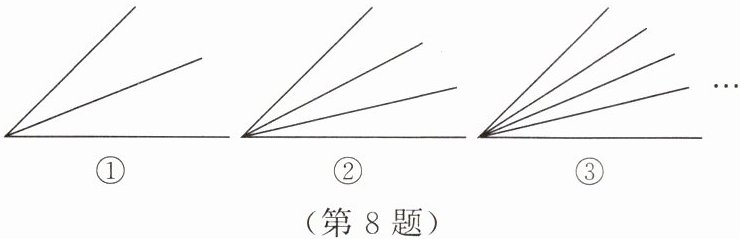
8. 图①中有3个角，图②中有6个角，图③中有10个角，依此类推，若一个角上有n条射线，共有$\frac{n(n-1)}{2}$个角。

答案： 3 6 10 $\frac{n(n-1)}{2}$

9. 如图，回答下列问题：
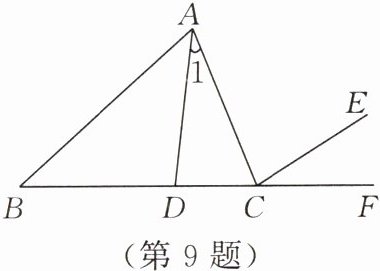
(1)$∠1$表示成$∠A$，这样的表示方法是否正确？如果不正确，应该怎样改正？
(2)图中哪个角可以用一个字母表示？
(3)以 A 为顶点的角有几个？请表示出来。
(4)$∠ADC$与$∠ACD$是同一个角吗？请说明理由。

答案： 解:
(1)不正确。以A为顶点的角有3个,故∠1不能用∠A表示,可表示成∠DAC。
(2)图中∠B可以用一个字母表示。
(3)以A为顶点的角有3个,分别是∠BAC,∠BAD,∠DAC。
(4)不是。因为这两个角的顶点不同。

10. (数学应用)日常生活中，我们几乎每天都要看钟表，它的时针和分针如同兄弟俩在赛跑，其中蕴含着丰富的数学知识。“元旦”这一天，城区某中学七年级部分学生上午八点多在学校门口集合，准备去步行街进行公益服务。临出发时，组长一看钟表，时针与分针正好重合。下午两点多他们回到学校。进校门时，组长看见钟表的时针与分针方向相反，正好成一条直线。那么你知道他们去步行街进行公益服务共用了多长时间吗？通过计算加以说明。

答案： 设上午8时x分时出发,下午2时y分回到学校,则$(12-1)× \frac{x}{60}× 30^{\circ }=8× 30^{\circ }$,解得$x=\frac{480}{11}\approx 44$,$(12-1)× \frac{y}{60}× 30^{\circ }-2× 30^{\circ }=180^{\circ }$,解得$y=\frac{480}{11}\approx 44$,所以共用6小时(上午大约8:44出发,下午大约2:44回校)。