第5页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
9. (综合与实践)两个完全相同的长方体,长、宽、高分别是5cm,4cm,3cm,把它们以不同方式叠放在一起,可以组成几种不同的新的长方体,在这几种新的长方体中,表面积最大是
164 cm²
。
答案:
164 cm²
10. (数学应用)如图①中所示的是3个形状完全相同的几何体(下底面为圆面,单位:cm)。将它们拼成如图②所示的新几何体,该新几何体的体积为

60π
。(结果保留π)
答案:
60π cm³
11. (综合与实践)小军和小红分别将直角梯形绕它的上底和下底所在直线旋转一周,得到两个立体图形。
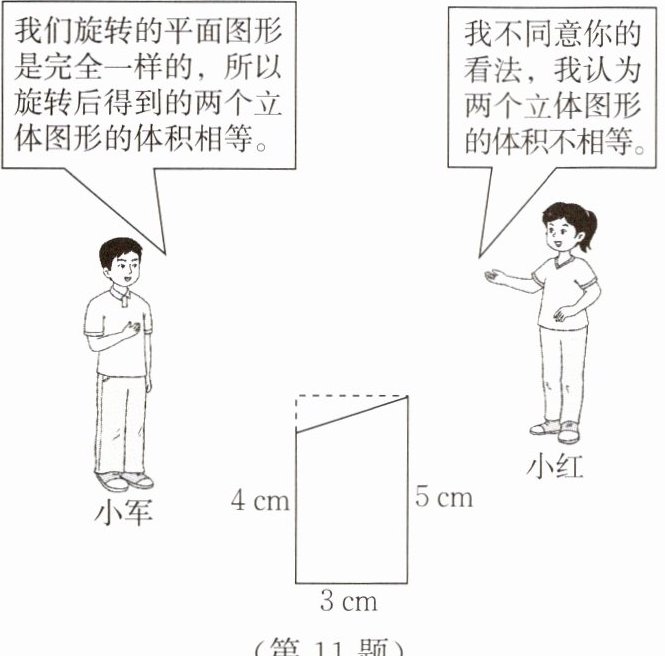
你同意

你同意
小红
的说法。与同伴交流,并说出你的理由。解:理由如下:绕4 cm长的上底所在直线旋转一周得到立体图形的体积为42π cm³,绕5 cm长的下底所在直线旋转一周得到立体图形的体积为39π cm³,42π cm³≠39π cm³。
答案:
解:小红 理由如下:绕4 cm长的上底所在直线旋转一周得到立体图形的体积为42π cm³,绕5 cm长的下底所在直线旋转一周得到立体图形的体积为39π cm³,42π cm³≠39π cm³。
12. 如图,大长方形的长为8cm,宽为6cm;小长方形的长为4cm,宽为3cm。以长边中点连线(图中虚线)为轴,将图中阴影部分旋转一周得到一个几何体,求这个几何体的表面积。(结果保留π)


答案:
1. 首先分析旋转后得到的几何体:
以长边中点连线为轴旋转一周后,得到的几何体是一个大圆柱(底面半径$R = 4cm$,高$h_1=6cm$)中间挖去一个小圆柱(底面半径$r = 2cm$,高$h_2 = 3cm$)。
圆柱的表面积公式$S = 2\pi R^{2}+2\pi Rh$($R$为底面半径,$h$为高)。
2. 然后计算大圆柱的表面积$S_1$:
大圆柱的两个底面积$S_{底1}=2\pi R^{2}$,其中$R = 4$,则$S_{底1}=2\pi×4^{2}=32\pi$。
大圆柱的侧面积$S_{侧1}=2\pi Rh_1$,$R = 4$,$h_1 = 6$,则$S_{侧1}=2\pi×4×6 = 48\pi$。
3. 接着计算小圆柱的侧面积$S_2$:
小圆柱的侧面积公式$S_{侧2}=2\pi rh_2$,其中$r = 2$,$h_2 = 3$,则$S_{侧2}=2\pi×2×3=12\pi$。
4. 最后计算组合体(所求几何体)的表面积$S$:
所求几何体的表面积$S=S_{底1}+S_{侧1}+S_{侧2}$。
把$S_{底1}=32\pi$,$S_{侧1}=48\pi$,$S_{侧2}=12\pi$代入可得:
$S=(32\pi + 48\pi+12\pi)cm^{2}$。
$S = 92\pi cm^{2}$。
所以这个几何体的表面积是$92\pi cm^{2}$。
以长边中点连线为轴旋转一周后,得到的几何体是一个大圆柱(底面半径$R = 4cm$,高$h_1=6cm$)中间挖去一个小圆柱(底面半径$r = 2cm$,高$h_2 = 3cm$)。
圆柱的表面积公式$S = 2\pi R^{2}+2\pi Rh$($R$为底面半径,$h$为高)。
2. 然后计算大圆柱的表面积$S_1$:
大圆柱的两个底面积$S_{底1}=2\pi R^{2}$,其中$R = 4$,则$S_{底1}=2\pi×4^{2}=32\pi$。
大圆柱的侧面积$S_{侧1}=2\pi Rh_1$,$R = 4$,$h_1 = 6$,则$S_{侧1}=2\pi×4×6 = 48\pi$。
3. 接着计算小圆柱的侧面积$S_2$:
小圆柱的侧面积公式$S_{侧2}=2\pi rh_2$,其中$r = 2$,$h_2 = 3$,则$S_{侧2}=2\pi×2×3=12\pi$。
4. 最后计算组合体(所求几何体)的表面积$S$:
所求几何体的表面积$S=S_{底1}+S_{侧1}+S_{侧2}$。
把$S_{底1}=32\pi$,$S_{侧1}=48\pi$,$S_{侧2}=12\pi$代入可得:
$S=(32\pi + 48\pi+12\pi)cm^{2}$。
$S = 92\pi cm^{2}$。
所以这个几何体的表面积是$92\pi cm^{2}$。
13. (综合与实践)【主题】卷筒纸的设计与测量
【素材】某品牌卷筒纸,直尺。
【实践操作】
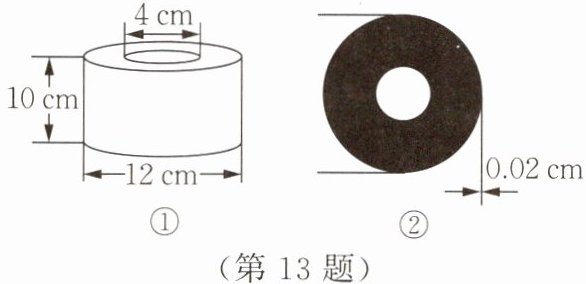
步骤1:使用直尺测量卷筒纸的高度,中间空心硬纸轴的直径和外层的直径,记录数据如图①所示。
步骤2:如图②,把展开的纸巾折叠多层后再测量,通过计算得到每层纸巾厚度为0.02cm。
【实践探索】
(1)制作这个中间的纸轴至少需要多少平方厘米的硬纸板?(结果保留π)
(2)根据以上数据,设计一个方案,估计这种规格的一卷空心卷筒纸展开后的总长度。(π的值取3.14)
【素材】某品牌卷筒纸,直尺。
【实践操作】
步骤1:使用直尺测量卷筒纸的高度,中间空心硬纸轴的直径和外层的直径,记录数据如图①所示。
步骤2:如图②,把展开的纸巾折叠多层后再测量,通过计算得到每层纸巾厚度为0.02cm。

【实践探索】
(1)制作这个中间的纸轴至少需要多少平方厘米的硬纸板?(结果保留π)
(2)根据以上数据,设计一个方案,估计这种规格的一卷空心卷筒纸展开后的总长度。(π的值取3.14)
答案:
1. (1)
解:求制作中间纸轴需要的硬纸板面积,就是求纸轴的侧面积。
圆柱侧面积公式为$S = \pi dh$($d$是底面直径,$h$是高)。
已知纸轴直径$d = 4cm$,卷筒纸高度$h = 10cm$。
则纸轴侧面积$S=\pi×4×10 = 40\pi(cm^{2})$。
2. (2)
解:方案如下:
先求卷筒纸的横截面积(圆环面积)$S=\pi R^{2}-\pi r^{2}$($R$是外层半径,$r$是纸轴半径)。
已知外层直径$D = 12cm$,则$R=\frac{12}{2}=6cm$;纸轴直径$d = 4cm$,则$r = \frac{4}{2}=2cm$。
所以圆环面积$S=\pi×6^{2}-\pi×2^{2}=\pi(36 - 4)=32\pi(cm^{2})$。
因为每层纸巾厚度$d_{0}=0.02cm$,设卷筒纸展开后的总长度为$L$。
由于卷筒纸展开后,横截面积$×$高度$=$体积,而体积也等于展开后长方体(长$×$宽$×$高,这里宽就是卷筒纸高度$h = 10cm$,长是卷筒纸展开长度$L$,高是纸巾厚度$d_{0}$)的体积,又因为横截面积$×$卷筒纸高度$=$展开后纸巾的体积(横截面积$×$卷筒纸高度$=L×$卷筒纸高度$×$每层纸巾厚度),在高度相同的情况下,横截面积$=L×$每层纸巾厚度。
则$L=\frac{S}{d_{0}}$($S$是圆环面积,$d_{0}$是每层纸巾厚度)。
把$S = 32\pi cm^{2}$,$d_{0}=0.02cm$,$\pi = 3.14$代入,$L=\frac{32×3.14}{0.02}$。
$L=\frac{32×3.14}{0.02}=\frac{100.48}{0.02}=5024(cm)$。
综上,(1)制作中间纸轴至少需要$40\pi cm^{2}$的硬纸板;(2)卷筒纸展开后的总长度约为$5024cm$。
解:求制作中间纸轴需要的硬纸板面积,就是求纸轴的侧面积。
圆柱侧面积公式为$S = \pi dh$($d$是底面直径,$h$是高)。
已知纸轴直径$d = 4cm$,卷筒纸高度$h = 10cm$。
则纸轴侧面积$S=\pi×4×10 = 40\pi(cm^{2})$。
2. (2)
解:方案如下:
先求卷筒纸的横截面积(圆环面积)$S=\pi R^{2}-\pi r^{2}$($R$是外层半径,$r$是纸轴半径)。
已知外层直径$D = 12cm$,则$R=\frac{12}{2}=6cm$;纸轴直径$d = 4cm$,则$r = \frac{4}{2}=2cm$。
所以圆环面积$S=\pi×6^{2}-\pi×2^{2}=\pi(36 - 4)=32\pi(cm^{2})$。
因为每层纸巾厚度$d_{0}=0.02cm$,设卷筒纸展开后的总长度为$L$。
由于卷筒纸展开后,横截面积$×$高度$=$体积,而体积也等于展开后长方体(长$×$宽$×$高,这里宽就是卷筒纸高度$h = 10cm$,长是卷筒纸展开长度$L$,高是纸巾厚度$d_{0}$)的体积,又因为横截面积$×$卷筒纸高度$=$展开后纸巾的体积(横截面积$×$卷筒纸高度$=L×$卷筒纸高度$×$每层纸巾厚度),在高度相同的情况下,横截面积$=L×$每层纸巾厚度。
则$L=\frac{S}{d_{0}}$($S$是圆环面积,$d_{0}$是每层纸巾厚度)。
把$S = 32\pi cm^{2}$,$d_{0}=0.02cm$,$\pi = 3.14$代入,$L=\frac{32×3.14}{0.02}$。
$L=\frac{32×3.14}{0.02}=\frac{100.48}{0.02}=5024(cm)$。
综上,(1)制作中间纸轴至少需要$40\pi cm^{2}$的硬纸板;(2)卷筒纸展开后的总长度约为$5024cm$。
查看更多完整答案,请扫码查看


