《2025年课堂精练七年级数学上册北师大版四川专版》

8. 计算：
(1)$\left(-3\dfrac{1}{2}\right)+4.8$； (2)$1+\left(-\dfrac{1}{2}\right)+\left(-\dfrac{1}{3}\right)$；
(3)$(-1.6)+\left(-3\dfrac{1}{5}\right)+|-1.8|$。

答案： 1. （1）
首先将带分数化为小数：
因为$-3\frac{1}{2}=-3.5$，所以$\left(-3\frac{1}{2}\right)+4.8=-3.5 + 4.8$。
根据有理数加法法则$a + b$（$a=-3.5$，$b = 4.8$，$\vert b\vert\gt\vert a\vert$），$a + b=\vert b\vert-\vert a\vert$（符号取$b$的符号），则$-3.5 + 4.8=4.8-3.5 = 1.3$。
2. （2）
解：
$1+\left(-\frac{1}{2}\right)+\left(-\frac{1}{3}\right)=1-\frac{1}{2}-\frac{1}{3}$。
先通分，$1=\frac{6}{6}$，$\frac{1}{2}=\frac{3}{6}$，$\frac{1}{3}=\frac{2}{6}$。
则$\frac{6}{6}-\frac{3}{6}-\frac{2}{6}=\frac{6 - 3-2}{6}=\frac{1}{6}$。
3. （3）
解：
先化简绝对值$\vert-1.8\vert = 1.8$，$-3\frac{1}{5}=-3.2$。
则$(-1.6)+\left(-3\frac{1}{5}\right)+\vert-1.8\vert=-1.6-3.2 + 1.8$。
利用加法结合律$(-1.6-3.2)+1.8=-4.8 + 1.8$。
根据有理数加法法则$a + b$（$a=-4.8$，$b = 1.8$，$\vert a\vert\gt\vert b\vert$），$a + b=-( \vert a\vert-\vert b\vert)$，所以$-4.8 + 1.8=-(4.8 - 1.8)=-3$。
综上，（1）的结果是$1.3$；（2）的结果是$\frac{1}{6}$；（3）的结果是$-3$。

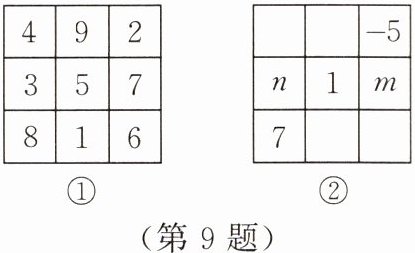
9. (数学文化)“九宫图”传说是远古时代洛河中一个神龟背上的图案，故称“龟背图”。观察图①，我们可以归纳出“九宫图”中各数之间的关系，即每行、每列及对角线上的$3$个数之和都相等。那么在图②中，$m+n=$2。

答案： 2

10. 给出下列说法：①两个数的和一定大于其中任何一个加数；②如果两个数的和是正数，那么这两个加数一定都是正数；③如果两个数的和为负数，则至少有一个加数是负数；④一个有理数与它的绝对值的和一定不是负数。其中正确的有③④。(填序号)

答案： ③④

11. 若有理数$x$，$y$满足$|x|=5$，$|y|=2$，且$|x+y|=x+y$，求$x+y$的值。

答案： 解：由|x|=5，得x=±5；由|y|=2，得y=±2。又因为|x+y|=x+y，所以x+y＞0或x+y=0，则x=5，y=±2。当x=5，y=2时，x+y=5+2=7；当x=5，y=-2时，x+y=5+(-2)=3。

12. (综合与实践)(1)比较大小；
①$|-2|+|3|$＞$|(-2)+3|$；
②$|4|+|3|$=$|4+3|$；
③$\left|-\dfrac{1}{2}\right|+\left|-\dfrac{1}{3}\right|$=$\left|\left(-\dfrac{1}{2}\right)+\left(-\dfrac{1}{3}\right)\right|$。
(2)通过(1)中大小比较，猜想并归纳出$|a|+|b|$与$|a+b|$的大小关系，进一步说明$a$，$b$满足什么关系时，$|a|+|b|=|a+b|$成立。
|a|+|b|与|a+b|的大小关系为|a+b|＜|a|+|b|或|a+b|=|a|+|b|；a，b满足同号或a，b中至少有1个为0时，|a+b|=|a|+|b|。

答案： 解：
(1)①＞ ②= ③=
(2)|a|+|b|与|a+b|的大小关系为|a+b|＜|a|+|b|或|a+b|=|a|+|b|；a，b满足同号或a，b中至少有1个为0时，|a+b|=|a|+|b|。

13. (综合与实践)请在如图所示的各个圆圈内填上适当的数，使每个圆圈里的数都等于与它相邻的两个数的和。

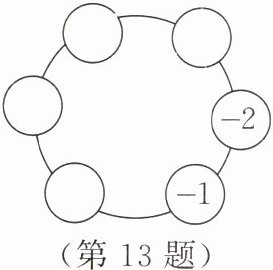
答案：
解：填数如图所示。