《2025年课堂精练七年级数学上册北师大版四川专版》

13. 先化简，再求值：$2(x^{2}y + 3xy) - 3(x^{2}y - 1) - 2xy - 2$，其中$x = -2$，$y = 2$。

答案： 解:原式=2x²y+6xy-3x²y+3-2xy-2=-x²y+4xy+1,当x=-2,y=2时,原式=-x²y+4xy+1=-(-2)²×2+4×(-2)×2+1=-23。

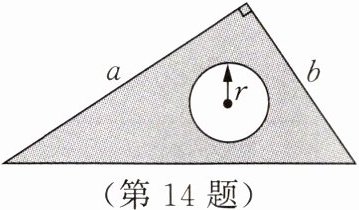
14. 一个塑料三角尺，形状和尺寸如图所示。
（1）求出阴影部分的面积；
（2）当$a = 5\ cm$，$b = 4\ cm$，$r = 1\ cm$时，计算出阴影部分的面积。（结果保留$\pi$）

答案： 解:
(1)S阴影=1/2ab-πr²。
(2)当a=5cm,b=4cm,r=1cm时,S阴影=1/2ab-πr²=1/2×5×4-π×1²=(10-π)(cm²)。

15. 解答下列问题：
（1）若代数式$2x + 3y$的值为$-5$，求代数式$4x + 6y + 3$的值；
（2）已知$A = 3x^{2} - 5x + 1$，$B = -2x + 3x^{2} - 5$，求当$x = \frac{1}{3}$时，$A - B$的值。

答案： 解:
(1)由题意得2x+3y=-5,则4x+6y+3=2(2x+3y)+3=-5×2+3=-7。
(2)A-B=3x²-5x+1-(-2x+3x²-5)=-3x+6,故当x=1/3时,原式=-3x+6=-3×1/3+6=5。

16.（数学应用）如图，$1$张餐桌可坐$6$人，$2$张餐桌可坐10人。

（1）按照上图的方式继续排列餐桌，填写下表：
|餐桌张数|1|2|3|4|5|6|
|----|----|----|----|----|----|----|
|可坐人数|6|10|14|18|22|26|
（2）摆$n$张餐桌时可坐多少人？用代数式表示。
4n+2
（3）一家餐厅有这样的长方形餐桌$30$张，按照上图方式每$5$张拼成一张大餐桌，共可坐多少人？若按上图方式每$6$张拼成一张大餐桌，则可坐多少人？若现在有$131$人就餐，则该用多少张这样的长方形餐桌拼成一张大餐桌？
由题意得:5张这样的长方形餐桌拼成一张大餐桌共可坐30÷5×(4×5+2)=132(人);6张这样的长方形餐桌拼成一张大餐桌共可坐30÷6×(4×6+2)=130(人)。由此可见,若131人就餐,需要5张这样的长方形餐桌拼成一张大餐桌。

答案： 解:10
(1)依次填:6,10,14,18,22,26
(2)4n+2
(3)由题意得:5张这样的长方形餐桌拼成一张大餐桌共可坐30÷5×(4×5+2)=132(人);6张这样的长方形餐桌拼成一张大餐桌共可坐30÷6×(4×6+2)=130(人)。由此可见,若131人就餐,需要5张这样的长方形餐桌拼成一张大餐桌。