《2025年创新课堂创新作业本七年级数学上册人教版》

14. 解方程：
(1)$\frac{1}{2}x + 3 = \frac{1}{3}x + 2$。
(2)$0.5x - 0.7 = 6.5 + 0.2x$。
(3)$1 - \frac{7}{3}x = \frac{2}{3}x + 19$。
(4)$0.4x - \frac{1}{4} = 8 - \frac{1}{5}x$。

答案： 解:
(1)x=-6.
(2)x=24.
(3)x=-6.
(4)x=$\frac{55}{4}$.

15. 小王看到两个商场的促销信息如表所示。

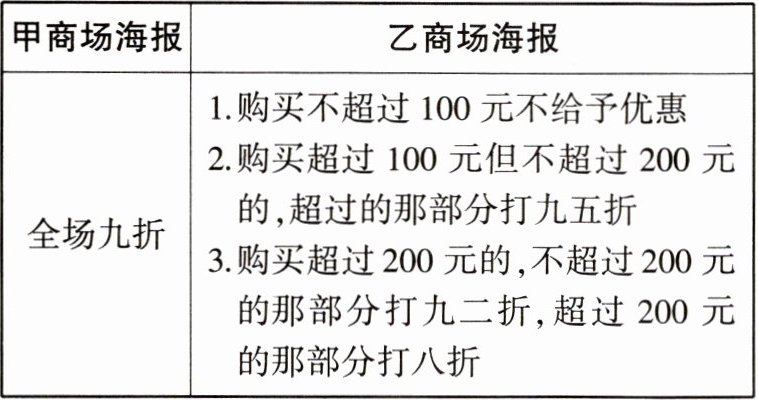
(1)当一次性购物标价总额是 200 元时,在甲、乙商场实际付款分别是多少元？
(2)当标价总额是多少元时,在甲、乙商场购物实际付款一样多？
(3)小王两次到乙商场分别购买标价 98 元和 150 元的商品,如果他想只去一次该商场购买这些商品,你能帮他计算可以节省多少钱吗？

答案： 解:
(1)甲商场实际付款200×0.9=180(元); 乙商场实际付款100+(200-100)×0.95=195(元).
(2)设标价总额为x元. 由题意,得在甲商场实际付款0.9x. 当x≤100时,在乙商场实际付款x元, 0.9x=x,解得x=0(不合题意,舍去); 当100＜x≤200时,在乙商场实际付款100+(x-100)×0.95=0.95x+5(元), 0.9x=0.95x+5,解得x=-100(不合题意,舍去); 当x＞200时,在乙商场实际付款200×0.92+(x-200)×0.8=0.8x+24(元), 0.9x=0.8x+24,解得x=240. 所以当标价总额是240元时,在甲、乙商场购物实际付款一样多.
(3)小王两次到乙商场需要付款98+(0.95×150+5)=245.5(元); 若小王只去一次乙商场,需要付款0.8×(98+150)+24=222.4(元). 故可节省245.5-222.4=23.1(元).

16. 核心素养·几何直观 定义：若 $A - B = m$,则称 $A$ 与 $B$ 是关于 $m$ 的关联数。例如：若 $A - B = 2$,则称 $A$ 与 $B$ 是关于 2 的关联数。
(1)若 3 与 $a$ 是关于 2 的关联数,则 $a = $1。
(2)若 $2x - 1$ 与 $3x - 5$ 是关于 2 的关联数,求 $x$ 的值。
解:根据题意,得2x-1-3x+5=2, 移项合并,得-x=-2, 解得x=2.
(3)若 $M$ 与 $N$ 是关于 $m$ 的关联数,$M = 3mn + n + 3$,$N$ 的值与 $m$ 无关,求 $N$ 的值。
解:根据题意,得M-N=m,即3mn+n+3-N=m,即3nm-m+n+3=N. 由于N的值与m无关,得3n-1=0,解得n=$\frac{1}{3}$,则N=$\frac{10}{3}$.

答案： 解:
(1)根据题意,得3-a=2,解得a=1.故答案为1.
(2)根据题意,得2x-1-3x+5=2, 移项合并,得-x=-2, 解得x=2.
(3)根据题意,得M-N=m,即3mn+n+3-N=m,即3nm-m+n+3=N. 由于N的值与m无关,得3n-1=0,解得n=$\frac{1}{3}$,则N=$\frac{10}{3}$.