《2025年创新课堂创新作业本七年级数学上册人教版》

13. 国庆期间,某广场上设置了一个庆祝国庆的造型(如图所示)。该造型平面呈轴对称,其正中间为一个半径为 $ b $ 的半圆,摆放花草,其余部分为展板。

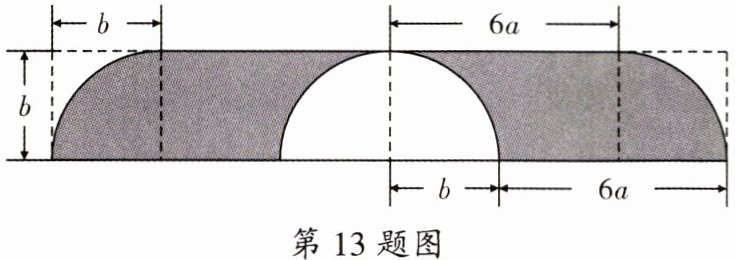
(1) 展板的面积是______12ab。(用含 $ a $,$ b $ 的代数式表示)
(2) 若 $ a = 1 $ m,$ b = 2 $ m。
① 求展板的面积；
② 已知摆放花草部分造价为 500 元/$ m^2 $,展板部分造价为 120 元/$ m^2 $,求制作整个造型的造价($ \pi $ 取 3.14)。
①当$a=1m$,$b=2m$时,展板的面积$=12×1×2=24(m^{2})$。②$120×24+500×π×2^{2}×\frac {1}{2}=2880+1000π\approx 2880+3.14×1000=6020$(元),即制作整个造型的造价为6020元。

答案： 解:
(1)根据题意,展板的面积为$2×6ab=12ab$.故答案为12ab.
(2)①当$a=1m$,$b=2m$时,展板的面积$=12×1×2=24(m^{2}).$②$120×24+500×π×2^{2}×\frac {1}{2}=2880+1000π\approx 2880+3.14×1000=6020$(元),即制作整个造型的造价为6020元.

14. 新情境 现代营养学家用身体质量指数衡量人体胖瘦程度,这个指数等于人体体重(单位：kg)与人体身高(单位：m)平方的商。对于成年人来说,身体质量指数在 18.5~24 之间,体重适中；身体质量指数低于 18.5,体重过轻；身体质量指数高于 24,体重超重。
(1) 设一个人的体重为 $ w $(单位：kg),身高为 $ h $(单位：m)。则他的身体质量指数 $ p = $$\frac{w}{h^2}$。(用含 $ w $,$ h $ 的代数式表示)
(2) 李老师的身高是 1.70 m,体重是 60 kg,他的体重是否适中？
解:把$h=1.70m$,$w=60kg$代入$\frac {w}{h^{2}}$,得李老师的身体质量指数为$\frac {60}{1.70^{2}}=20.76$.因为$18.5＜20.76＜24$,所以他的体重适中.

答案： 解:
(1)根据题意,他的身体质量指数$p=\frac {w}{h^{2}}$.故答案为$\frac {w}{h^{2}}$.
(2)把$h=1.70m$,$w=60kg$代入$\frac {w}{h^{2}}$,得李老师的身体质量指数为$\frac {60}{1.70^{2}}=20.76$.因为$18.5＜20.76＜24$,所以他的体重适中.

15. 核心素养·推理能力 某公园中的一条小路是用正六边形、正方形、正三角形三种地砖按照如图所示的方式铺设而成的,第 1 个图案中有 1 块正六边形地砖、6 块正方形地砖和 6 块正三角形地砖；第 2 个图案中有 2 块正六边形地砖、11 块正方形地砖和 10 块正三角形地砖……

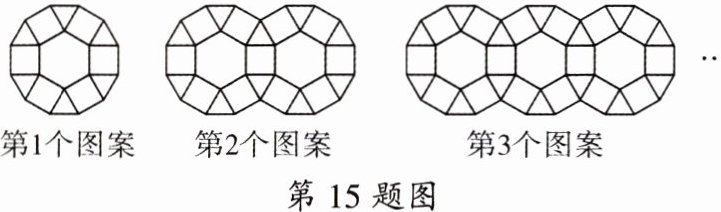
(1) 每增加一块正六边形地砖,正方形地砖会增加5块,正三角形地砖会增加4块。
(2) 若铺设这条小路共用去 $ n $ 块正六边形地砖,则共用去了$1+5n$块正方形地砖,$2+4n$块正三角形地砖。(分别用含 $ n $ 的代数式表示)
(3) 当 $ n = 30 $ 时,求正方形地砖和正三角形地砖的总数量。
解:当$n=30$时,正方形地砖的数量为$1+5×30=151$(块),正三角形地砖的数量为$2+4×30=122$(块),$151+122=273$(块).答:正方形地砖和正三角形地砖的总数量为273块.

答案： 解:
(1)每增加一块正六边形地砖,正方形地砖会增加$11-6=5$(块),正三角形地砖会增加$10-6=4$(块).故答案为5,4.
(2)由题意可知用去n块正六边形地砖时,共用去了$(1+5n)$块正方形地砖,$(2+4n)$块正三角形地砖.故答案为$(1+5n)$,$(2+4n)$.
(3)当$n=30$时,正方形地砖的数量为$1+5×30=151$(块),正三角形地砖的数量为$2+4×30=122$(块),$151+122=273$(块).答:正方形地砖和正三角形地砖的总数量为273块.