第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
10. 跨学科· 信息技术 按如图所示的运算程序,若输入 $ m $ 的值是 $ -3 $,则输出的结果是 (

A.$ 0 $
B.$ -3 $
C.$ 8 $
D.$ 9 $
D
)
A.$ 0 $
B.$ -3 $
C.$ 8 $
D.$ 9 $
答案:
D
11. 当 $ x = 3 $,$ y = -2 $ 时,求下列代数式的值.
(1) $ x^2 - y^2 $.
(2) $ \frac{x + y}{x - y} $.
(3) $ x^2 - 2xy + y^2 $.
(4) $ 3x^2 - \frac{5}{2}y $.
(1) $ x^2 - y^2 $.
(2) $ \frac{x + y}{x - y} $.
(3) $ x^2 - 2xy + y^2 $.
(4) $ 3x^2 - \frac{5}{2}y $.
答案:
解:当$x=3,y=-2$时,
(1)$x^{2}-y^{2}=9-4=5$.
(2)$\frac{x+y}{x-y}=\frac{3-2}{3+2}=\frac{1}{5}$.
(3)$x^{2}-2xy+y^{2}=9+12+4=25$.
(4)$3x^{2}-\frac{5}{2}y=27+5=32$.
(1)$x^{2}-y^{2}=9-4=5$.
(2)$\frac{x+y}{x-y}=\frac{3-2}{3+2}=\frac{1}{5}$.
(3)$x^{2}-2xy+y^{2}=9+12+4=25$.
(4)$3x^{2}-\frac{5}{2}y=27+5=32$.
12. 如图,图 $ 1 $ 有 $ 1 $ 个正三角形,图 $ 2 $ 有 $ 5 $ 个正三角形,图 $ 3 $ 有 $ 9 $ 个正三角形……则图 $ n $ 中正三角形的个数是 (
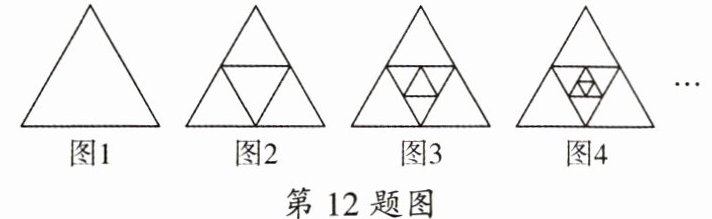
A.$ 2n - 1 $
B.$ 4n - 3 $
C.$ 4n - 2 $
D.$ 3n - 2 $
B
)
A.$ 2n - 1 $
B.$ 4n - 3 $
C.$ 4n - 2 $
D.$ 3n - 2 $
答案:
B
13. 如图是一组有规律的图案组成的“小鱼”图形,它由若干根火柴棒组成. 第 $ 1 $ 个图案由 $ 8 $ 根火柴棒组成,第 $ 2 $ 个图案由 $ 14 $ 根火柴棒组成,第 $ 3 $ 个图案由 $ 20 $ 根火柴棒组成,第 $ 4 $ 个图案由 $ 26 $ 根火柴棒组成……依此规律,第 $ n $ 个图案由
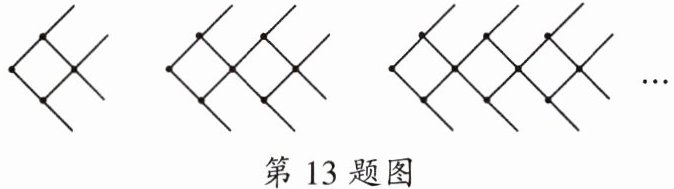
$(6n+2)$
根火柴棒组成. ( 用含 $ n $ 的代数式表示 )
答案:
$(6n+2)$
14. 新情境 今年小辰家买了新的房子,他们想将家里的地板按照如下划分贴上 $ 4 $ 种不同图案的瓷砖.
(1) 用含 $ a $,$ b $ 的代数式表示小辰家地板的面积 $ S $.
(2) 若 $ a = 3 $,$ b = 6 $,且贴瓷砖每平方米需要花费 $ 45 $ 元,则小辰家贴瓷砖共需花费多少钱?

(1) 用含 $ a $,$ b $ 的代数式表示小辰家地板的面积 $ S $.
(2) 若 $ a = 3 $,$ b = 6 $,且贴瓷砖每平方米需要花费 $ 45 $ 元,则小辰家贴瓷砖共需花费多少钱?

答案:
解:
(1)$S=2ab+a^{2}+\frac{1}{2}b^{2}(m^{2})$.
(2)当$a=3,b=6$时,$S=2×3×6+3^{2}+\frac{1}{2}×6^{2}=63(m^{2})$,所以$63×45=2835$(元).答:小辰家贴瓷砖共需花费2835元.
(1)$S=2ab+a^{2}+\frac{1}{2}b^{2}(m^{2})$.
(2)当$a=3,b=6$时,$S=2×3×6+3^{2}+\frac{1}{2}×6^{2}=63(m^{2})$,所以$63×45=2835$(元).答:小辰家贴瓷砖共需花费2835元.
15. 【观察思考】

【规律发现】
(1) 请用含 $ n $ 的代数式填空:
上述是由正八边形构成的图案,正八边形的每个顶点上都有“★”或“▲”. 第 $ n $ 个图案中“★”有
【规律应用】
(2) 在第 $ 2024 $ 个图案中,求“★”的数量比“▲”的数量多多少个.

【规律发现】
(1) 请用含 $ n $ 的代数式填空:
上述是由正八边形构成的图案,正八边形的每个顶点上都有“★”或“▲”. 第 $ n $ 个图案中“★”有
4n
个,“▲”有1+3n
个.【规律应用】
(2) 在第 $ 2024 $ 个图案中,求“★”的数量比“▲”的数量多多少个.
解:(2)在第2024个图案中,“★”的数量为$4×2024=8096$(个),“▲”的数量为$1+3×2024=6073$(个),$8096-6073=2023$(个).答:“★”的数量比“▲”的数量多2023个.
答案:
解:
(1)$4n$,$1+3n$.
(2)在第2024个图案中,“★”的数量为$4×2024=8096$(个),“▲”的数量为$1+3×2024=6073$(个),$8096-6073=2023$(个).答:“★”的数量比“▲”的数量多2023个.
(1)$4n$,$1+3n$.
(2)在第2024个图案中,“★”的数量为$4×2024=8096$(个),“▲”的数量为$1+3×2024=6073$(个),$8096-6073=2023$(个).答:“★”的数量比“▲”的数量多2023个.
查看更多完整答案,请扫码查看


