《2025年创新课堂创新作业本七年级数学上册人教版》

1. 填表：

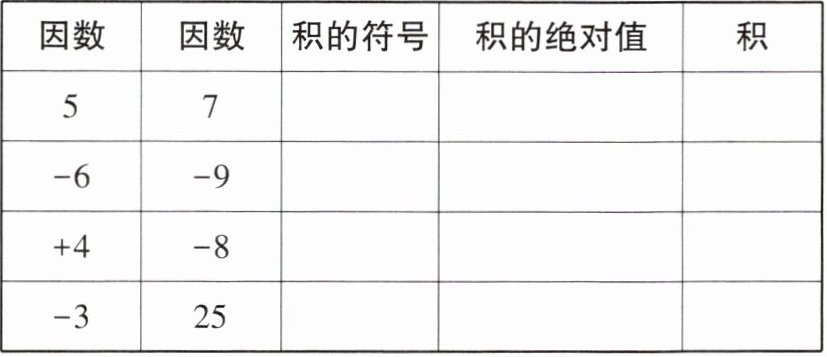
因数 因数 积的符号 积的绝对值 积
5 7 + 35 +35
-6 -9 + 54 +54
+4 -8 - 32 -32
-3 25 - 75 -75

答案： 因数 因数 积的符号 积的绝对值 积
5 7 + 35 +35
-6 -9 + 54 +54
+4 -8 - 32 -32
-3 25 - 75 -75

2. 计算$(-4)×\frac{3}{2}$的结果是(A)
A.-6
B.6
C.-8
D.8

答案： A

3. 对于$(-5)×7$,左边第一个因数增加1后积的变化是(D)
A.减少5
B.增加5
C.减少7
D.增加7

答案： D

4. 若$a$,$b满足\vert a - 2\vert+\vert b + 3\vert = 0$,则$ab= $-6。

答案： -6

5. 计算：
(1) $(-3)×(-24)$。
(2) $(-1000)×0.1$。
(3) $(-12.5)×(-0.8)$。
(4) $0×(-0.375)$。

答案： 解:
(1)原式=3×24=72.
(2)原式=-1000×0.1=-100.
(3)原式=12.5×0.8=10.
(4)原式=0.

6. $-\frac{1}{2}$的倒数是(A)

A.-2
B.$-\frac{1}{2}$
C.2
D.$\frac{1}{2}$

答案： A

7. 下列两个数互为倒数的是(C)
A.4和-4
B.-3和$\frac{1}{3}$
C.-2和$-\frac{1}{2}$
D.0和0

答案： C

8. 若$□×(-5)= 1$,则$□$内应填的数是(D)
A.$\frac{1}{5}$
B.5
C.-5
D.$-\frac{1}{5}$

答案： D

9. (1) -4的倒数是$-\frac{1}{4}$,$-\frac{1}{7}$的倒数是$-7$,6的倒数的相反数是$-\frac{1}{6}$。
(2) 倒数等于它本身的数是$\pm1$。

答案： 1. 首先求$-4$的倒数：
根据倒数的定义：若两个数的乘积是$1$，我们就称这两个数互为倒数。设$-4$的倒数为$x$，则$-4x = 1$，解得$x=-\frac{1}{4}$。
2. 然后求$-\frac{1}{7}$的倒数：
设$-\frac{1}{7}$的倒数为$y$，则$-\frac{1}{7}y = 1$，解得$y=-7$。
3. 接着求$6$的倒数的相反数：
先求$6$的倒数，设$6$的倒数为$z$，则$6z = 1$，解得$z=\frac{1}{6}$。
再求$\frac{1}{6}$的相反数，根据相反数的定义：绝对值相等，正负号相反的两个数互为相反数，所以$\frac{1}{6}$的相反数是$-\frac{1}{6}$。
4. 最后求倒数等于它本身的数：
设这个数为$a$，则$a× a = 1$，即$a^{2}=1$。
解方程$a^{2}=1$，根据平方根的定义$a=\pm\sqrt{1}=\pm1$，当$a = 1$时，$1$的倒数是$1$；当$a=-1$时，$-1$的倒数是$-1$。
故答案依次为：$-\frac{1}{4}$；$-7$；$-\frac{1}{6}$；$\pm1$。

10. 写出下列各数的倒数：3,-1,0.3,$-\frac{2}{3}$,$\frac{1}{4}$,$-2\frac{1}{2}$。

答案： 1. 首先明确倒数的定义：
若两个数的乘积是$1$，我们就称这两个数互为倒数。即若$a× b = 1$，则$a=\frac{1}{b}(b\neq0)$，$b = \frac{1}{a}(a\neq0)$。
2. 然后求各数的倒数：
对于$3$：
设$3$的倒数为$x$，则$3x = 1$，解得$x=\frac{1}{3}$。
对于$-1$：
设$-1$的倒数为$y$，则$-1× y = 1$，解得$y=-1$。
对于$0.3=\frac{3}{10}$：
设$0.3$的倒数为$m$，则$\frac{3}{10}m = 1$，根据$m = 1÷\frac{3}{10}$，由除法运算法则$a÷ b=a×\frac{1}{b}(b\neq0)$，可得$m = 1×\frac{10}{3}=\frac{10}{3}$。
对于$-\frac{2}{3}$：
设$-\frac{2}{3}$的倒数为$n$，则$-\frac{2}{3}n = 1$，解得$n=1÷(-\frac{2}{3})=1×(-\frac{3}{2})=-\frac{3}{2}$。
对于$\frac{1}{4}$：
设$\frac{1}{4}$的倒数为$p$，则$\frac{1}{4}p = 1$，解得$p = 4$。
对于$-2\frac{1}{2}=-\frac{5}{2}$：
设$-2\frac{1}{2}$的倒数为$q$，则$-\frac{5}{2}q = 1$，解得$q=1÷(-\frac{5}{2})=1×(-\frac{2}{5})=-\frac{2}{5}$。
所以$3$的倒数是$\frac{1}{3}$；$-1$的倒数是$-1$；$0.3$的倒数是$\frac{10}{3}$；$-\frac{2}{3}$的倒数是$-\frac{3}{2}$；$\frac{1}{4}$的倒数是$4$；$-2\frac{1}{2}$的倒数是$-\frac{2}{5}$。