《2025年创新课堂创新作业本七年级数学上册人教版》

11. 若$y$是未知数,解方程$my = 3.5$时,方程两边同时乘$-4$,使未知数的系数变为$1$,则$m = $$-\frac{1}{4}$。

答案： $-\frac{1}{4}$

12. 数学文化 幻方的历史悠久,传说最早出现在夏禹时代的“洛书”中,把“洛书”用今天的数学符号翻译出来,就是一个三阶幻方,三阶幻方的每行、每列、每条对角线上的三个数之和都相等。如图是一个三阶幻方,则$a - b$的值为______。

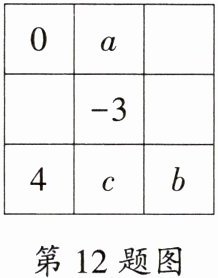
7

答案： 7

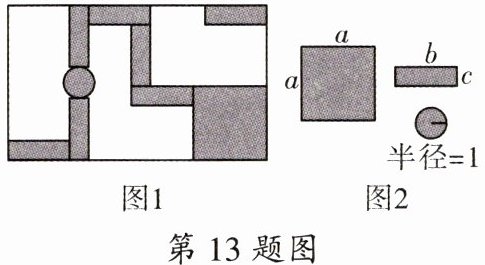
13. 如图1,在一块长方形区域中布置了图中阴影部分所示的展区,其中的展台有三种不同的形状,其规格如图2所示。根据图中信息,用等式表示$a$,$b$,$c$满足的关系为a-b+c=2。

答案： a-b+c=2

14. 若$a^{2} - 2a = 1$,求下列各式的值：
(1)$2a^{2} - 4a + 6$。
(2)$-\frac{1}{4}a^{2} + \frac{1}{2}a - 10$。

答案： 解:
(1)原式=2($a^2-2a$)+6=2×1+6=8.
(2)$-\frac{1}{4}a^2+\frac{1}{2}a-10=-\frac{1}{4}(a^2-2a)-10=-\frac{1}{4}×1-10=-10\frac{1}{4}$.

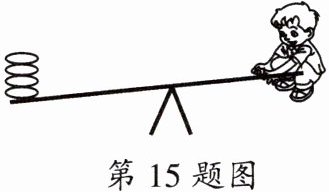
15. 如图,跷跷板的一端放置4个相同质量的沙包,体重为45kg的阿豪坐在另一端压不上来,当他怀抱1个同样质量的沙包时,跷跷板恰好保持平衡。设每个沙包的质量为$x$kg。
(1) 请你列出一个含有未知数$x$的方程。
(2) 利用等式的性质求出$x$的值。

答案： 解:
(1)由题意,得4x=x+45.
(2)根据等式的性质1,得4x-x=45,
即3x=45,根据等式的性质2,得x=15.

16. 在下面的表格中,从左到右依次在每个小方格中填入一个数,使得其中任意三个相邻方格中所填数之和都相等,例如：$a + b + x = b + x + (-2)$。

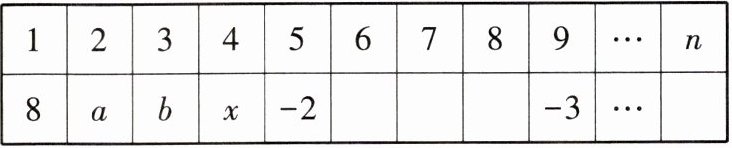
(1) 求出第4格中的数$x$。
(2) 第6格中的数是______-3。

答案： 解:
(1)因为任意三个相邻格子中所填数之和都相等,
所以8+a+b=a+b+x,所以x=8.
(2)-3
(3)因为表格中的数字以8,-2,-3循环,且三个重复数字的和为3,
又2024÷3=674……2,所以第2024个格子中的数是-2,
所以前2024个格子中所填各数之和为674×3+8+(-2)=2028.