《2025年创新课堂创新作业本七年级数学上册人教版》

10. 定义一种新运算“$*$”,规定运算法则为$m*n = m^{n} - mn$($m$,$n$均为整数,且$m\neq 0$)。例如：$2*3 = 2^{3} - 2× 3 = 2$,则$(-2)*2 = $8。

答案： 8

11. 跨学科·信息技术 某兴趣小组设计了一种计算机程序图,根据程序图回答下列问题：
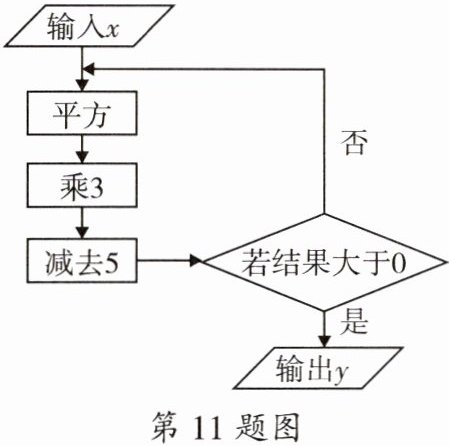
(1)当$x = 3$时,则输出$y = $22。
(2)当$x = -1$时,则输出$y = $7。

答案：
(1)22
(2)7

12. 数学文化 远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”。如图,一位母亲在从右到左依次排列的绳子上打结,满七进一(从右往左进位),用来记录孩子自出生后的天数。由图可知,这个孩子自出生后的天数是501。

答案： 501

13. 计算：
(1)$(-2)^{3}× 8 - 8× (\frac{1}{2})^{3} + 8× \frac{1}{8}$。
(2)$(-3)^{2} - \frac{1}{6}× 5 + \frac{1}{6}× (-3^{2})$。
(3)$-2^{4} + \frac{1}{2}× [6 + (-4)^{2}]$。

答案：
(1)原式=(-8-$\frac{1}{8}$+$\frac{1}{8}$)×8=-64.
(2)原式=9-$\frac{1}{6}$×(5+9)=$\frac{20}{3}$.
(3)原式=-16+$\frac{1}{2}$×22=-5.

14. 若$|2 + a| + |b - 3| = 0$,$c的倒数与d$互为相反数,$e$比最大的负整数小4,求$-a^{b} + \frac{1}{c} - e + d$的值。

答案： 解:因为|2+a|+|b-3|=0,|2+a|≥0,|b-3|≥0, 所以2+a=0,b-3=0,解得a=-2,b=3. 因为c的倒数为$\frac{1}{c}$,且与d互为相反数, 所以$\frac{1}{c}$+d=0. 因为最大的负整数为-1,且e比最大的负整数小4, 所以e=-1-4=-5, 所以-aᵇ+$\frac{1}{c}$-e+d=-(-2)³+($\frac{1}{c}$+d)-e=8+0-(-5)=13.

15. (1)欲求$1 + 2 + 3 + 4 + … + n$的值,可令$S = 1 + 2 + 3 + 4 + … + n$①,将①式右边顺序倒置,得$S = n + … + 4 + 3 + 2 + 1$②。由②+①,得$2S = $$n(n+1)$,所以$S = $$\frac{n(n+1)}{2}$。由结论求$1 + 2 + 3 + 4 + … + 100 = $5050。
(2)①观察一列数2,4,8,16,32,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是2。根据此规律,如果$a_{n}$($n$为正整数)表示这个数列的第$n$项,那么$a_{18} = $$2^{18}$,$a_{n} = $$2^{n}$。
②为了求$1 + 3 + 3^{2} + 3^{3} + … + 3^{2018}$的值,可令$M = 1 + 3 + 3^{2} + 3^{3} + … + 3^{2018}$①,则$3M = 3 + 3^{2} + 3^{3} + … + 3^{2019}$②。由②-①,得$3M - M = 3^{2019} - 1$,所以$M = \frac{3^{2019} - 1}{2}$,即$1 + 3 + 3^{2} + 3^{3} + … + 3^{2018} = \frac{3^{2019} - 1}{2}$。
仿照以上推理,计算$1 + 5 + 5^{2} + 5^{3} + … + 5^{51}$。
令M=1+5+5²+5³+…+5⁵¹①,则5M=5+5²+5³+…+5⁵¹+5⁵²②. 由②-①,得5M-M=5⁵²-1,M=$\frac{5⁵²-1}{4}$, 即1+5+5²+5³+…+5⁵¹=$\frac{5⁵²-1}{4}$.

答案： 解:
(1)2S=(n+1)+(n+1)+…+(n+1)=n(n+1),S=$\frac{n(n+1)}{2}$, n个(n+1) 1+2+3+4+…+100=$\frac{100×(100+1)}{2}$=5 050. 故答案为n(n+1),$\frac{n(n+1)}{2}$,5 050.
(2)①这个常数是2.a₁₈=2¹⁸,aₙ=2ⁿ. 故答案为2,2¹⁸,2ⁿ. ②令M=1+5+5²+5³+…+5⁵¹①,则5M=5+5²+5³+…+5⁵¹+5⁵²②. 由②-①,得5M-M=5⁵²-1,M=$\frac{5⁵²-1}{4}$, 即1+5+5²+5³+…+5⁵¹=$\frac{5⁵²-1}{4}$.